|
Title:
Packing Density of Voice Trunking using AAL2
Abstract:
In this contribution, we study the effect of CPS Timer_ CU value on the packing density of voice trunking using AAL2. Assuming ITU G.723.1 is used for voice encoding, we set up a Markov chain model to analyze the AAL2 packing process. We find that the packing density, which is directly linked to link efficiency, depends on the Timer_ CU value and number of users in the system. The analysis of this contribution gives an algorithm to calculate a reference Timer_ CU value to achieve desired link efficiency.
Source:
Chunlei Liu, Sohail Munir, Raj Jain
Department of Computer and Information Science
The Ohio State University, Columbus, OH 43210-1277
email:
{
cliu,munir,jain
}
@cse.wustl.edu
Sudhir Dixit
Nokia Research Center
3 Burlington Woods Dr., Suite 250, Burlington, MA 01803
email: sudhir.dixit@research.nokia.com
This presentation of this contribution is sponsored by NASA Lewis Research Center.
This research was sponsored in part by US Army CECOM Contract DAAB08-98-C-B305.
Date:
November 29 - December 4, 1998
Distribution:
ATM Forum Technical Committee
VTOA, TM working groups
Notice:
This contribution has been prepared to assist the ATM Forum. It is offered to the Forum as a basis for discussion and is not a binding proposal on the part of any of the contributing organizations. The statements are subject to change in form and content after further study. Specifically, the contributors reserve the right to add to, amend or modify the statements contained herein.
In ATM_ Forum contribution 98-0630[ 3], Kevin Zhang analyzed the effect of the CPS Timer_ CU value on packet delay variation (PDV), and found the CPS Timer_ CU value is not relevant in total PDV calculation. By considering the talkspurt and packet arrival pattern, we found that while the statement about PDV is correct, the Timer_ CU value has to be set appropriately since it significantly affects the link efficiency.
Timer_ CU value determines the time after which a cell should be dispatched, even if it is not fully packed. If the value is too small, more partial cells are likely to be sent and the link efficiency will be low. If it is too large, some packets will suffer prolonged delay and the voice quality will degrade.
In this contribution, we set up a Markov chain model to analyze the packing process of AAL2 using G.723.1 voice encoding. The Markov analysis reveals the correlation between successive cells and gives a formula for calculating the packing density based on the Timer_ CU value and the number of voice sources in the system.
To validate our analytic result, a NetSim simulation was launched to actually implement the AAL2 packing process. The results of simulation confirm our analysis. They are presented in the last section.
The result of this contribution allows us to choose an appropriate Timer_ CU value according to the number of voice sources to improve link efficiency.
|
The parameter Timer_ CU is used to avoid prolonged delay in case no packets arrive for a long period. When the first packet is put in the cell, the Timer_ CU is started. If the cell is not fully packed within the Timer_ CU time, the cell (timer) " expires " and the partially packed cell is sent.
If the working cell is partially packed and an arriving packet can not fit in the remaining space, the first part of the packet is put into the remaining space and the remainder will be put in the next cell. The Timer_ CU for the next cell is started at the arrival of this packet.
The cells go through the links and switches and arrive at the destination AAL2. The destination AAL2 will unpack the cells and dispatch each packet to its destination according to the channel identifier(CID) contained in the mini-header of the packet.
Human voice consists of alternating talkspurts and silence intervals. It has been found that talkspurt length and silence interval are exponentially distributed[ 1]. In a commonly accepted model, the talkspurts have a mean length of 352 ms and silence intervals have a mean length of 650 ms [ 2].
There a number of standards for coding voice before transmission over the networks. ITU G.723.1 is currently the most widely used encoding standard. During talkspurts, G.723.1 sends out a 20-byte packet every 30 ms. During silence periods, no packets are sent. In this contribution, we assume all voice sources use G.723.1 as the encoding method.
Compared with the talkspurt length and silence period, the 30 ms packet length is quite short. This means, during a talkspurt, the arrival of the packets from one voice source is highly predictable.
Suppose that the number of voice sources in the system is
N
and that a packet has just been received from a voice source. We want to calculate the probability of no packet arrival from all sources in the next
 ms, where
ms, where
 is the Timer_ CU value.
is the Timer_ CU value.
Consider one voice source first. During an average 352 ms talkspurt and 650 ms silence cycle, an average of 12 packets need to be sent as shown in Figure 2.
|
Let
s
denote the number of packets generated during a talkspurt interval. In order to have no packet arrival in
 ms, the starting point of this
ms, the starting point of this
 ms cannot fall in the
ms cannot fall in the
 ms interval before any of these
s
arrivals. The probability of no packet arrival from this source is
ms interval before any of these
s
arrivals. The probability of no packet arrival from this source is
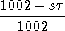
 <
30. On the average, the probability of no packet arrival from one source is
<
30. On the average, the probability of no packet arrival from one source is
Voice sources are assumed to be independent. After the receipt of the first packet in the cell, the probability of no packet arrival from all other sources within
 ms is
ms is
The probability of one packet arrival from all other sources is
After we have the probability R 0 , R 1 , we can now calculate the average packing density.
The average number of bytes in an AAL2 cell depends on whether there is a remainder from the last cell and how many packets are received since the first packet is put in the cell. Let r n be a random variable to denote the remainder length left from the ( n - 1)th cell. Since each packet has a 3-byte header and a 20-byte payload, the remainder bytes are always less than 23 bytes, i.e., 0 < r n < 22. This value is exactly the STF field in the n th AAL2 cell.
Event r n = 0 happens only when cell n - 1 expires or when r n - 1 = 1 and cell n - 1 does not expire.
Event r n = 1 happens only when r n - 1 = 2 and cell n - 1 does not expire.
Event r n = 2 happens only when r n - 1 = 3 and cell n - 1 does not expire.
. . . . . .
Event r n = 22 happens only when r n - 1 = 0 and cell n - 1 does not expire.
Therefore, { r n } is a Markov chain. Consider the stationary state where all { r n } have the same probability distribution. Let r be any of these r n , denote
and
Since an AAL2 cell has 47 bytes payload, and for G.723.1 a CPS packet has 23 bytes, it happens that for all i = 0 , . . . , 22,
Denote
then the transition matrix is
In stationary distribution,
So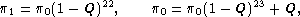
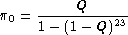
Using these probabilities, we can find the average number of bytes in the AAL2 cell is
Because each 20-byte voice packet has a 3 bytes mini-header and each AAL2 cell has a 6-bytes overhead, the packing density is therefore,
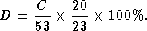 (12)
(12)
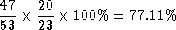
To validate our analysis, we wrote a NetSim simulation program to actually implement the AAL2 packing process. The simulation model is described in Section 2. The results of 11 simulations are summarized in Table 1. The first column is the Timer_ CU value used in the simulation. The second column is the total number of cells being sent. Column 3, 4 and 5 are the number of cells that have 0, 1, 2 or more packet arrivals since the packing of the first packet. The average density calculated from the total number of bytes in all cells is listed in the last column.
Table 1: Simulation results: number of packets received within
|
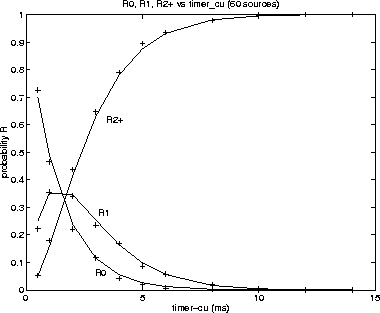
Figure 3: R 0 , R 1 and R 2 + for different Timer_ CU values. 60 sources. solid line: calculation; "+": simulation. |
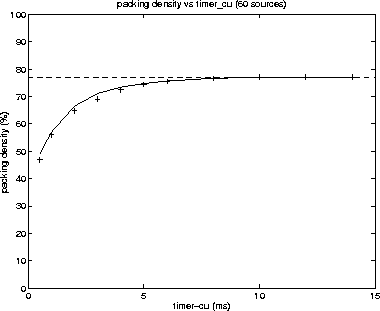
Figure 4: Packing density for different Timer_ CU values. 60 sources. solid line: calculation; "+": simulation. |
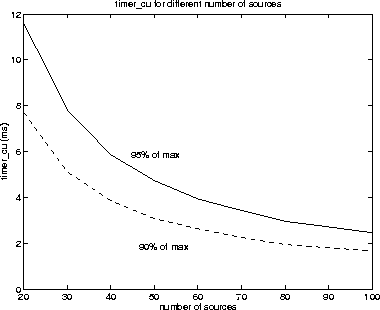
Figure 5: Timer_ CU values to reach 90% and 95% of the maximum packing density. |
[1] Paul T. Brady, A model for generating ON-OFF speech patterns in two-way conversations. Bell System Technical Journal , Vol 48, pp 2445-2472, Sept 1969.
[2] Shuang Deng, Traffic characteristics of packet voice, IEEE International Conference on Communications , Vol 3, pp 1369-1374, 1995.
[3] Kevin Zhang, Packet Delay Variation in Voice Trunking using AAL2, ATM Forum contribution 98-0630 , October 4-9, 1998, Australia.