| Garrison Prinslow, gprinslow@gmail.com (A paper written under the guidance of Prof. Raj Jain) |
Download |
Keywords: Multi-core processors, multi-core CPUs, performance measurement, performance modeling and analysis, benchmarking, parallelism, gprof, TAU, profiling.
Understanding the behavior and architecture of a multi-core processor is necessary to proficiently analyze its performance [Chandramowlishwaran10]. This section defines a multi-core processor, introduces the primary types of multi-core processors used in computing, then compares two of the most prevalent types used in performance computing contexts. The next section introduces three types of parallelism that impact multi-core processor performance. Subsequent sections apply these concepts in a performance analysis context, introducing techniques for performance measurement and analytical modeling. This paper assumes that the analyst is examining the performance of a given application on a multi-core processor, or different types of multi-core processors, seeking to quantify and understand why certain performance characteristics are observed.
This subsection defines a multi-core processor in general terms, discusses why multi-core processors emerged in the mainstream marketplace, and provides examples of common multi-core processors. Accordingly, this will provide the analyst with sufficient background to identify multi-core processors in a system before analyzing the appropriate performance implications.
To define a multi-core processor, a definition of a processor (or "microprocessor") is necessary as well. In computing terms, a processor is a component that reads and executes program instructions; these instructions tell the processor what to do, such as reading data from memory or sending data to an output bus [Microprocessor]. A common type of processor is the Central Processing Unit (CPU). A multi-core processor is generally defined as an integrated circuit to which two or more independent processors (called cores) are attached [Multi-core processor]. This term is distinct from but related to the term multi-CPU, which refers to having multiple CPUs which are not attached to the same integrated circuit [Multi-core processor]. The term uniprocessor generally refers to having one processor per system [Uniprocessor], and that the processor has one core [Keckler09]; it is used to contrast with multiprocessing architectures, i.e. either multi-core, multi-CPU, or both. Figure 1, below, illustrates the basic components of a generic multi-core processor.
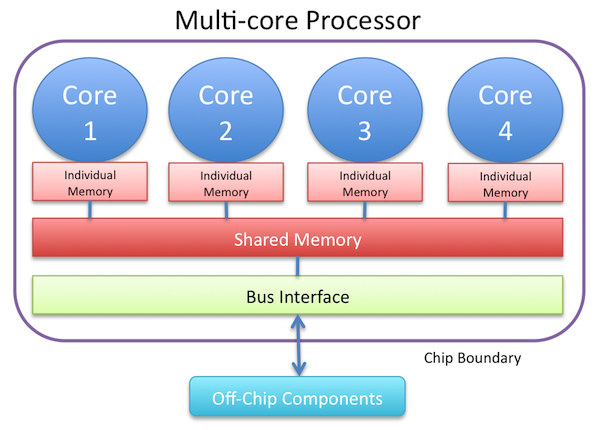
Figure 1: A basic block diagram of a generic multi-core processor
Multi-core processors emerged in the computing industry from uniprocessor technology as a method to achieve greater performance through parallelism rather than raw clock speed. Over the last 30 years, the computer industry developed faster and faster uniprocessors, though this pursuit is drawing to a close due to the limits of transistor scaling, power requirements, and heat dissipation [Keckler09]. Because single-threaded cores are reaching a plateau of clock frequency, chip manufacturers have turned to multi-core processors to enhance performance using parallelism [Keckler09].
So far this paper has discussed multi-core processors in a generic sense, as there are many specific types of multi-core processors serving varying functions in computing. Though it is common to refer to multi-core CPUs, other examples include Graphics Processing Units (GPUs) and Field Programmable Gate Arrays (FPGAs).
Modern GPUs have hundreds of cores, though these cores are significantly different from a CPU core. For example, NVIDIA's GeForce GTX 580 has 512 Compute Unified Device Architecture (CUDA) cores operating at 1544 MHz [NVIDIA:GTX 580]. AMD's competing Radeon HD 6970 has 1536 stream processors operating at 880 MHz [AMD:HD 6970]. GPUs are primarily designed to accelerate 3D graphics, but starting as early as 1999, computer scientists and researchers recognized that the relatively high floating point performance in GPUs could be used to accelerate other scientific computational applications [NVIDIA:GPU Computing]. The term General Purpose computing/computation on GPUs (GPGPU) now refers to the use of GPUs for other applications besides traditional 3D graphics [Zibula09].
FPGAs might also be considered multi-core processors because this specialized hardware may be programmed to employ multiple "soft" microprocessor cores on one FPGA board [Multi-core processor]. The flexibility of reconfigurable hardware allows the FPGA board's configuration to be optimized for individual applications, rather than a traditional CPU which must have a universal instruction set. An example of an advanced multi-core CPU implemented on an FPGA board is the Open Scalable Processor Architecture (OpenSPARC) project; the T2 version implements eight 64-bit cores with individual Level 1 (L1) and shared Level 2 (L2) cache, and can run programs similarly to a traditional CPU [Sun:OpenSPARC T2].
Multi-core processors also exist in other forms, such as Digital Signal Processors (DSPs), game consoles, and networking hardware [Multi-core processor]. This paper will focus on multi-core CPUs, but it is important for the analyst to recognize the similarities and differences of multi-core CPUs to other multi-core processors, such as GPUs and FPGAs.
Recent studies focused on optimizing the performance of certain types of applications have claimed from 25x to 100x or more performance speedup by utilizing GPUs instead of CPUs for the primary computation task [Lee10]. While this paper will be focusing on multi-core CPU performance, it is important to briefly contrast this with GPGPU performance, as the analyst may need to consider both areas considering the prevalence of GPGPU approaches in high performance computing.
While the speedup numbers of these studies using a GPGPU strategy are dramatic, CPUs and GPUs are designed to be efficient at significantly different types of tasks. The architectural differences between CPUs and GPUs cause CPUs to perform better on latency-sensitive, partially sequential, single sets of tasks [Lee10]. In contrast, GPUs perform better with latency-tolerant, highly parallel and independent tasks [Lee10]. Depending on the application being studied, the overall performance may be better or worse on a GPU, or the latencies may be unacceptable even if throughput is relatively high.
This section defined a multi-core processor then compared the key types of multi-core processors for performance computing. Accordingly, the analyst may identify the relevant types of multi-core processors involved in a particular problem. The next section will introduce the types of parallelism employed by multi-core CPUs to increase performance, and subsequent sections will apply these concepts to performance measurement and analytical modeling.
Because multi-core CPUs exploit parallelism to enhance performance, an understanding of the key types of parallelism is important to analyzing performance. Parallelism is a complex topic but a basic understanding of three types of parallelism is sufficient here. Instruction-level parallelism, thread-level parallelism, and data-level parallelism are all employed by various multi-core CPU architectures, and have different impacts on performance that must be understood to conduct thorough performance analysis.
The first key type of parallelism, instruction-level parallelism (or ILP), involves executing certain instructions of a program simultaneously which would otherwise be executed sequentially [Goossens10], which may positively impact performance depending on the instruction mix in the application.
Most modern CPUs utilize instruction-level parallelization techniques such as pipelining, superscalar execution, prediction, out-of-order execution, dynamic branch prediction or address speculation [Goossens10]. However, only certain portions of a given program's instruction set may be suitable for instruction-level parallelization, as a simple example illustrates below in Figure 2. Because steps 1 and 2 of the sequential operation are independent of each other, a processor employing instruction-level parallelism can run instructions 1.A. and 1.B. simultaneously and thereby reduce the operation cycles to complete the operation by 33%. The last step must be executed sequentially in either case, however, as it is dependent on the two prior steps.

Figure 2: A simple example of instruction-level parallelism
This example is an oversimplification, but it generally conveys both the potential benefit and potential limits of the technique. For the analyst, the key is to understand which portions of an application have instructions that could run in parallel.
The second key type of parallelism, thread-level parallelism (or TLP), involves executing individual task threads delegated to the CPU simultaneously [Blake10][Ahn07]. Thread-level parallelism will substantially impact multi-threaded application performance through various factors, ranging from hardware-specific, thread-implementation specific, to application-specific, and consequently a basic understanding is important for the analyst.
Each thread maintains its own memory stack and instructions, such that it may be thought of as an independent task, even if in reality the thread might not really be independent in the program or operating system. Thread-level parallelism is used by programs and operating systems that have a multi-threaded design. Conceptually, it is straightforward to see why thread-level parallelism would increase performance. If the threads are truly independent, then spreading out a set of threads among available cores on a processor would reduce the elapsed execution time to the maximum execution time of any of the threads, compared to a single threaded version which would require additive execution time of all of the threads. Ideally, the work would also be evenly divided among threads, and the overhead of allocating and scheduling threads is minimal. Figure 3, below, illustrates these conceptual differences between single threading and thread-level parallelism, assuming independence and no additional per-thread overhead.
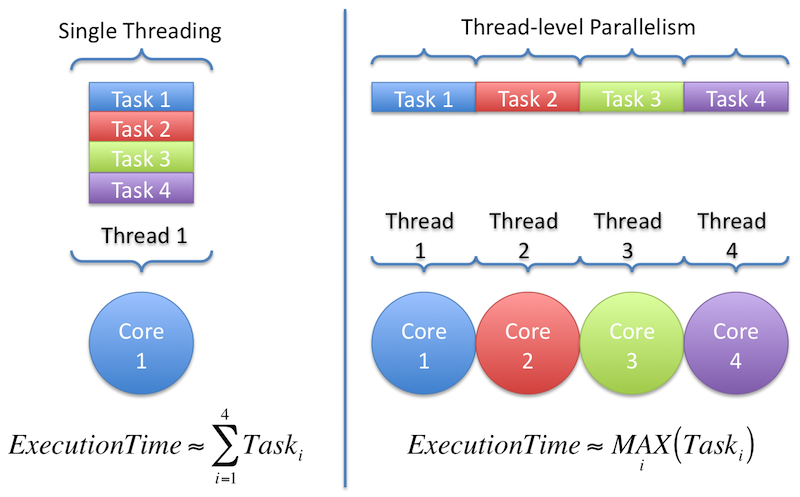
Figure 3: A conceptual visualization of thread-level parallelism
This simplistic ideal model of thread-level parallelism performance is complicated by several other factors, such that the ideal scenario is rarely observed in real applications. Performance-impacting factors include the load balance, level of execution independence, thread-locking mechanisms, scheduling methods, and thread memory required. Further, data-level parallelism among the distributed threads may impact performance, as the subsequent section discusses. The thread implementation library in both the operating system and the specific application will also impact performance [Blake10][Moseley07]. Consequently, an analyst examining an application with thread-level parallelism may need to control or regress these factors to quantify multi-core performance of the multi-threaded application.
The third key type of parallelism, data-level parallelism (or DLP), involves sharing common data among executing processes through memory coherence, improving performance by reducing the time required to load and access memory [Ahn07]. For the analyst, identifying application areas utilizing data-level parallelism will assist in understanding performance characteristics on multi-core processors.
In the context of a multi-core CPU, data-level parallelism in the cache memory shared by cores can have a substantial impact on performance [Chandramowlishwaran10][Ahn07]. Here, the executing processes running on multiple cores will be called threads. Performance gains are expected when the threads read from the same data in the shared memory. This scenario allows one copy of the data to be used by the multiple threads, reducing the number of copy operations and thus execution time. When the threads have no data in common, each thread must maintain a copy of its data and no gains are available. However, if the multiple requests to this memory exceed its bandwidth, increasing threads may produce negative performance impacts.
Further performance impacts may also occur during write operations. Multiple threads attempting to write to the same memory location at the same time must wait to resolve conflicts. Schemes to handle such situations are well known in computer science, such as spin-locks. The performance impact will depend upon the penalties involved with the scheme employed and how often such conflicts occur. Generally speaking, having threads write to different areas of shared memory would be preferable in lessening the likelihood of incurring these penalties. Non-Uniform Memory Architecture (NUMA) may assist, as it places data used by one particular core physically closer to that core in memory [Chandramowlishwaran10]. Bandwidth may also be an important factor as the number of threads increases on a multi-core processor.
Limited cache size (cache misses), limited bandwidth, off-cache latency, and other aspects will have impacts on performance, though data-level parallelism can improve performance in certain situations. Further, the interaction between instruction-level and data-level parallelism affects performance; Flynn's taxonomy is a useful framework to analyze these interactions [Flynn72]. In summary, observations about data-level parallelism in a particular application are crucial to analyzing its performance on multi-core CPUs because memory is frequently the limiting factor.
This section introduced three key types of parallelism employed by multi-core to enhance performance. Instruction-level parallelism, thread-level parallelism, and data-level parallelism have varying performance impacts, and consequently understanding, identifying, and studying these factors will lead to improved performance analysis. The next section introduces tools for empirically measuring and benchmarking multi-core CPUs, then provides an example that uses these tools and the concepts in prior sections, using empirical measurements to make performance observations.
Performance analysis commonly involves benchmarking and empirically measuring performance to validate or assist with creating analytical models of performance [Jain91]. This section will introduce tools for empirically measuring and benchmarking multi-core CPUs. It will then provide an example that builds upon the concepts in prior sections, using empirical measurements to make performance observations about the multi-core CPU involved. The tools introduced will be focused on the Linux environment, both because this platform is common in high-performance computing and to suit the example provided.
Provided there is an existing application and a multi-core CPU available for testing, the analyst may use performance measurement tools to gain insight into the processor's performance characteristics. This subsection will introduce three common tools that are used to profile an existing application's performance, beginning with simpler tools that provide basic information and continuing into more advanced tools.
It should be noted that, in general, the more profiling data that is collected, the more the profiling overhead impacts the performance of the actual application [Moseley07]. Therefore, profiling is best used as a tool to understand performance behavior, especially while varying experimental factors, rather than to measure absolute performance. For any rule there is also an exception; methods for low-overhead, highly-informative profiling are an area of ongoing research and include hardware and parallelized approaches [Moseley07].
One of the most basic measures of performance is how much elapsed time an application takes from the user's submitted request to the system's completed response, or response time. [Jain91]. In a Linux/UNIX environment, the time command provides a straightforward way to measure elapsed time of any command (e.g. an application's run command) [Kernel]. It also provides the user CPU time and system CPU time, defined as the total number of CPU-seconds the process spent in user mode and kernel mode respectively [Kernel]. This information may be considered "coarse grained" because it only provides the total time spent running the command, rather than data about the time spent in individual function calls. In a multi-core CPU context, gathering elapsed time measurements while varying the number of threads for a multi-threaded application will provide high-level information on the speedup provided from parallelization. Unlike several other tools discussed in this section, the time command does not require recompiling the source code to support gathering data.
GNU gprof provides an increase in profiling information that may be useful to the analyst while being straightforward to begin using. gprof is a tool included with the open source GCC package for compiling common programming languages, such as C, C++, and Java. gprof provides basic profiling information, such as the number of calls to functions within a program, the time spent within each function, cumulative time spent, and a graph showing parent-child function call relationships [GNUgprof]. However, except for the call numbers which are counted, the other statistics are sampled and subject to statistical inaccuracy [GNUgprof]. Moreover, gprof was not designed for multi-threading applications, and does not collect data on a per-thread basis [GNUgprof]. Therefore, its results are of limited utility to the performance analyst studying a multi-threaded application on a multi-core CPU.
Tuning and Analysis Utilities (TAU) is an open source, full featured profiling tool designed to collect performance data for multi-threaded programs written in Fortran, C++, C, Java, and Python [TAU]. Profiling an application with TAU can help answer important multi-core performance questions such as what functions account for the most time, whether threads are getting disproportionate amounts of work (load imbalance), how well the application scales as threads are increased, what loops account for the most time, and how many MFlops are used in the different loops [TAU]. Like gprof, providing instrumentation hooks for TAU requires recompiling an application's source code. Unlike gprof, TAU provides a Graphical User Interface (GUI) to assist with visualization of the performance data that drills down into more detail. For the analyst, TAU has a robust profiling toolset that will assist in gaining insight into an application's performance on a multi-core CPU.
This subsection introduced three common tools used to measure and profile an existing application's performance, which help characterize performance behavior of multi-threaded applications on multi-core CPUs. The next subsection will introduce benchmarking tools that enable the analyst to directly compare the performance of multi-core CPUs or estimate performance for an application that does not yet exist.
This subsection will introduce benchmarking tools that enable the analyst to directly compare the performance of multi-core CPUs and estimate performance for an application that does not yet exist. With some knowledge of the probable types of applications the multi-core CPU will be used for, a performance analyst may make useful comparisons between multi-core CPUs using benchmarks.
Prior sections of this paper have assumed that the performance analyst is examining the impact of a multi-core CPU on a particular application's performance, especially multi-threaded applications. Here, a different set of tools will allow a more isolated analysis of a particular CPU's performance. For example, the performance analyst may need to compare multiple models of multi-core CPUs to calculate an optimal price-performance tradeoff for an acquisition decision. The performance analyst might only have a general idea of the types of applications the workstation will run.
An industry standard benchmark, such as the benchmarks maintained and published by Standard Performance Evaluation Corporation (SPEC), provides a relative measure of performance in different types of computations [Jain91]. A practitioner may compile and run the benchmarks themselves or reference existing published results for many different multi-core CPUs [SPEC]. Comparing these benchmark scores across multi-core CPUs will consequently provide useful predictions of relative performance if the benchmark is representative of the type of task. For example, in the SPEC CPU2006 suite, CINT2006 tests integer arithmetic by running code that heavily utilizes integer arithmetic; this includes compilers, artificial intelligence, discrete event simulation, gene sequencing using Hidden Markov Models, and others [SPEC]. CFP2006 tests floating point operations with tests from fluid dynamics, quantum chemistry, physics, weather, speech recognition, and others [SPEC].
Though these two benchmarks will give a relative measure of raw CPU power in a given core, the focus of these tests is not parallelized workloads. For measuring parallel performance of multi-core CPUs, the SPEC OMP2001 and SPEC MPI2007 benchmarks are more applicable [SPEC]. The OMP2001 benchmark evaluates parallel performance of applications using Open Multi-Processing (OpenMP), which is a commonly used standard for multi-platform shared-memory parallel programming [SPEC][OpenMP]. Similarly, the MPI2007 benchmark evaluates parallel performance of compute intensive applications using Message Passing Interface (MPI) [SPEC]. For the analyst, benchmarks provided by the type of multi-threading package that will be used by a potential application would be more relevant.
In the context of multi-core CPUs, analysts may utilize benchmarking tools to get relative performance information among different multi-core CPU models across varying types of applications. The closer these types of applications are to ones run on the system being analyzed, the more relevant the results. The next subsection will provide examples that use empirical measurements to make performance observations about the multi-core CPU involved.
This subsection will provide an example of how to use measurements to analyze the performance of a multi-threaded application running on a multi-core CPU. The measurements can validate insights gained from other techniques and lead to new performance observations that otherwise might have been overlooked. This particular example is a numerical solution to Laplace's equation which has multi-threaded code implemented with OpenMP.
This example will investigate the performance of a numerical solution to Laplace's equation. Solutions to Laplace's equation are important in many scientific fields, such as electromagnetism, astronomy, and fluid dynamics [Laplace's equation]. Laplace's equation is also used to study heat conduction as it is the steady-state heat equation. This particular code solves the steady state temperature distribution over a rectangular grid of m by n points. It is written in C and implements OpenMP for multi-threading [Quinn10].
Examining the code of this application provides some initial insight into its expected performance behavior on a multi-core processor. Here, this particular code indicates that it is probably compute-intensive rather than memory-intensive. It visits each point, replacing the current point average with the weighted average of its neighbors. It uses a random walk strategy and continues iterating until the solution reaches a stable state, i.e. the difference between the current solution and the prior solution is less than a desired threshold epsilon. The higher the precision desired, the slower the convergence, and the number of iterations required is approximately 18/epsilon. At default values, this would require approximately 18,000 iterations. The largest memory required is two matrices of m by n double datatypes (8 bytes), so at the default of a 500 by 500 matrix, the memory requirements are relatively low. Because of the high number of iterations and computations per iteration, compared with relatively low memory requirements, this application is probably more compute-intensive than memory-intensive.
Further observations may be made about expected behavior using concepts of parallelism. First, we know that this application is implemented to utilize thread-level parallelization through OpenMP. Examining the code reveals that the initialization of values, calculation loops, and most updates (except calculating the current iteration difference compared to epsilon) are multi-threaded. Second, thinking about the way the code executes leads to some expected data-level parallelism. During an iteration each point utilizes portions of the same m by n matrix to calculate the average of its neighbors before writing an updated value. Therefore, we would expect some data-level parallelism benefit if threads/cores are sharing memory. The impact of instruction-level parallelism will depend upon the details of the multi-core processor architecture and the type of instruction mix. This particular example was executed on an Intel Core 2 Quad Q6600 (2.40 GHz, 4 Cores, 4 Threads, 8MB L2 Cache, 1066MHz Front Side Bus (FSB)) which includes several types of instruction-level parallelizations. The principal calculation in the code involves the averaging of four double-precision floating point numbers, then storing the result. Based on high-level literature, it would appear that the Intel Core architecture's Wide Dynamic Execution feature would allow each core to execute up to four of these instructions simultaneously [Doweck06]. Using the code and conceptual understanding of thread-, data-, and instruction-level parallelism can lead to useful insights about expected performance.
The next step is to use measurement techniques to confirm our expectations and gain further insights. Here we will focus on measuring the impact of thread-level parallelism by measuring execution time while varying the number of threads used by the application. The following results in Table 1, below, were obtained by executing the application on an Intel Q6600 quad core (four thread) CPU, varying the number of threads, while profiling the application using gprof and measuring the elapsed execution time using the time command.
Table 1: gprof data and execution time for varying thread count on a quad-core CPU
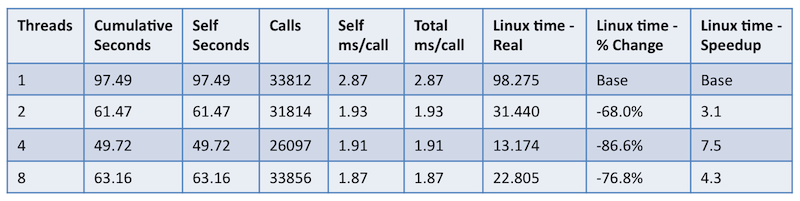
From these measurements the following observations can be made. First, taking a single-thread execution as the base, we see a significant elapsed execution time improvement by moving to two threads (-68.0% or 3.1x improvement) and four threads (-86.6% or 7.5x improvement). This validates our expectation regarding thread-level parallelism; because this application employs parallelization for the majority of its routines, performance would improve significantly by assigning additional processor cores to threaded work. We also gain an additional observation that the threading overhead is significant to performance, because increasing the number of threads from 4 to 8, twice the number of available cores in the CPU, degrades the overall performance by 73% compared to 4 threads (-76.8% or 4.3x improvement over 1 thread).
This is just one example of how measurements can assist with analyzing the performance of a particular application on a multi-core CPU. If the application exists and can be tested, measurements are a robust technique to make performance observations, validate assumptions and predictions, and gain a greater understanding of the application and multi-core CPU.
Performance measurements assist the analyst by quantifying the existing performance of an application. Through profiling tools, the analyst can identify the areas of an application that significantly impact performance, quantify speedups gained by adding threads, determine if work is evenly divided, and gain other important insights. In the next section, these empirical observations will be supported with analytical models that assist with predicting performance under certain assumptions.
This section introduces analytical techniques for modeling the performance of multi-core CPUs. These techniques generate predicted performance under certain assumptions which would then validate measurements collected [Jain91]. Conversely, measurements can validate the analytical models generated earlier, which is a more common sequence when a system or application does not yet exist. The three subsections introduce Amdahl's law, Gustafson's law, and computational intensity in the context of multi-core CPU performance, with examples for illustration.
This subsection will introduce Amdahl's law in the context of multi-core CPU performance and apply the law to the earlier example application that calculates Laplace's equation. Though it was conceived in 1967, long before modern multi-core CPUs existed, Amdahl's law is still being used and extended in multi-core processor performance analysis; for example, to analyze symmetric versus asymmetric multi-core designs [Hill08] or to analyze energy efficiency [Woo08].
Amdahl's law describes the expected speedup of an algorithm through parallelization in relationship to the portion of the algorithm that is serial versus parallel [Amdahl67]. The higher the proportion of parallel to serial execution, the greater the possible speedup as the number of processors (cores) increases. This law also expresses the possible speedup by when the algorithm is improved. Subsequent authors have summarized Amdahl's textual description with the following equations in Figure 4, where f is the fraction of the program that is infinitely parallelizable, n is the number of processors (cores), and S is the speedup of the parallelizable fraction f [Hill08].
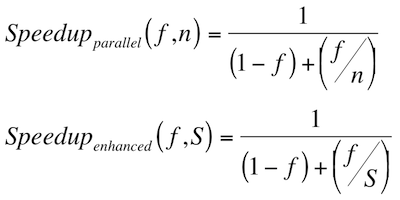
Figure 4: Amdahl's law - equations for speedup achieved by parallelization
These relatively simple equations have important implications for modern multi-core processor performance, because it places a theoretic bound on how much the performance of a given application may be improved by adding execution cores [Hill08]. The application from section 3.3 for Laplace's equation provides an illustration of Amdahl's law below in Figure 6. Here, the first value for f, the fraction of the program that is infinitely parallelizable, was chosen to be 0.95; the remaining 0.05 is sequentially executed. For this particular program that value is a pessimistic assumption, as the vast majority of execution time is spent in the parallelized loops, not in the single-threaded allocation or epsilon synchronization. For comparison, an optimistic value for f is also graphed at 0.9999, such that only 0.0001 (one-hundredth of a percent) is sequential. The observed values from the prior example for up to 4 cores (processors) are also plotted.
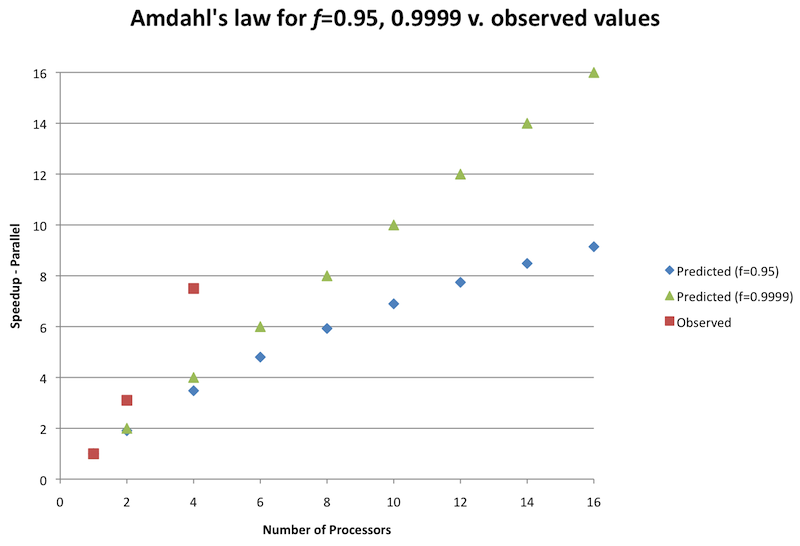
Figure 5: Amdahl's law for f=0.95, 0.9999 versus observed values
From this illustration it is clear that the predicted speedups according to Amdahl's law are pessimistic compared to our observed values, even with an optimistic value for f. At this point it is important to discuss several significant assumptions implicit in these equations. The primary assumption is that the computation problem size stays constant when cores are added, such that the fraction of parallel to serial execution remains constant [Hill08]. Other assumptions include that the work between cores is and can be evenly divided, and that there is no parallelization overhead [Hill08].
Even with these assumptions, in the context of multi-core processors the analytical model provided by Amdahl's law gives useful performance insights into parallelized applications [Hill08]. For example, if our goal is to accomplish a constant size problem in as little time as possible, within certain resource constraints, the area of diminishing returns in performance can be observed [Hill08]. Limited analytical data is required to make a prediction, i.e. the fraction of serial to parallel execution, which makes it a useful estimation early on in a decision process. However, our analysis goal might instead be to evaluate whether a very large size problem could be accomplished in a reasonable amount of time through parallelization, rather than minimize execution time. The next subsection will discuss Gustafson's law which is focused on this type of performance scenario for multi-core processors [Hill08].
This subsection introduces Gustafson's law in the context of multi-core CPU performance, contrasts it with Amdahl's law, and applies the law to the earlier example for illustration and comparison.
Gustafson's law (also known as Gustafson-Barsis' law) follows the argument that Amdahl's law did not adequately represent massively parallel architectures that operate on very large data sets, where smaller scales of parallelism would not provide solutions in tractable amounts of time [Hill08]. Here, the computation problem size changes dramatically with the dramatic increase in processors (cores); it is not assumed that the computation problem size will remain constant. Instead, the ratio of parallelized work to serialized work approaches one [Gustafson88]. The law is described by the equation in Figure 6 below, where s' is the serial time spent on the parallel system, p' is the parallel time spent on the parallel system, and n is the number of processors [Gustafson88].
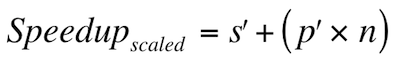
Figure 6: Gustafson's law - equation for scaled speedup
This law was proposed by E. Barsis as an alternative to Amdahl's law after observing that three different applications running on a 1024-processor hypercube experienced a speedup of about 1000x, for sequential execution percentages of 0.4-0.8 percent [Gustafson88]. According to Amdahl's law, the speedup should have been 200x or less. Gustafson's law operates on the assumption that when parallelizing a large problem, the problem size is increased and the run time is held to a constant, tractable level. This proposal generated significant controversy and renewed efforts in massively parallel problem research that would have seemed inefficient according to Amdahl's law [Hill08][Gustafson88].
Applying Gustafson's law to our earlier example provides a prediction that by increasing problem size and processors (cores), and keeping our desired time constant, we will achieve speedups roughly proportional to the number of processors. Here, in Figure 7, we used the same portion of parallel time (0.95) to serial time (0.05) to compare the graph of Gustafson's law and Amdahl's law for up to 16 processors. The observed values from the prior example for up to 4 cores (processors) are also plotted.
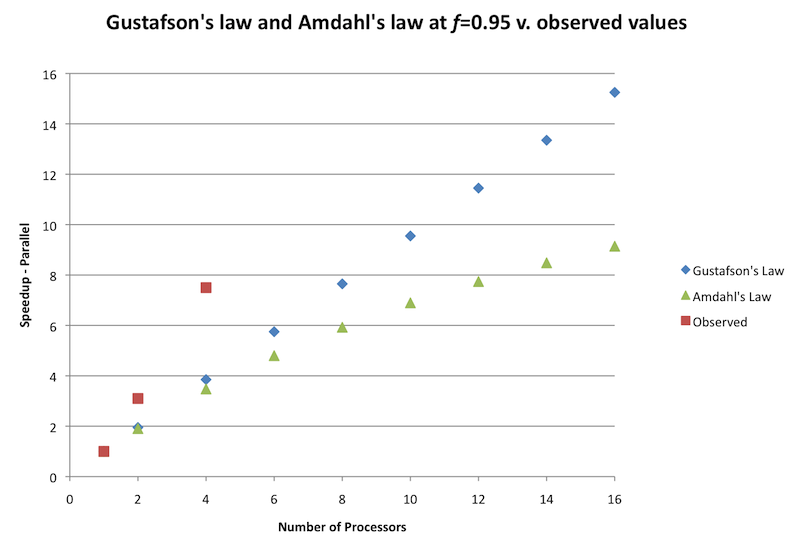
Figure 7: Gustafson's law and Amdahl's law at f=0.95 versus observed values
From the graph it is evident that Gustafson's law is more optimistic than Amdahl's law about the speedups achieved through parallelization on a multi-core CPU, and that the curve is similar to the speedups observed in this particular example. Another implication is that the amount of time spent in the serial portion becomes less and less significant as the number of processors (and problem size) is increased.
For the analyst, Gustafson's law is a useful approximation of potential speedups through parallelization when the data set is large, the problem is highly parallelizable, and the goal is to solve the problem within a set amount of time that would otherwise be unacceptably long [Hill08]. The next subsection introduces analytical techniques for computational intensity that can assist with formulating a more concrete performance bound for a given problem.
This subsection will introduce analytical techniques for determining computational and memory intensity in the context of multi-core CPU performance. This section draws heavily upon the well illustrated, step-by-step approach in [Chandrawmowlishwaran10], and the interested reader is encouraged to refer to their work for a detailed example of multi-core performance analysis regarding a multi-threaded implementation of the Fast Multipole Method. This subsection will be illustrated with a simple example derived from the Laplace's equation problem explored in prior sections.
Modeling computations in terms of compute intensity and memory intensity is a low-level technique to analyze the probable bottleneck of a given portion of an application. It is focused on answering the question whether that portion is compute-bound or memory-bound, such that performance improvements can be focused on the most limiting factor [Chandramowlishwaran10]. It can also provide probable answers to whether the memory required for a given portion would fit in the CPU cache; cache misses are expensive because of the additional delay involved with accessing system Random Access Memory (RAM), and identifying this problem may guide optimizations to reduce cache misses [Chandramowlishwaran10].
The analysis of computational intensity often begins with examining the asymptotic bounds of the algorithm, as this provides an upper bound on the growth rate of the function as the problem size n increases to infinity. This will provide an upper bound on the number of computations per n. The next step is to inspect the source code to approximately count the number of operations for each computation. Next, for a given operation, the number and type of instructions that would be executed by the CPU for each operation is counted. Then, taking into account possible instruction level parallelism, instruction latencies, and throughputs specific to the particular processor architecture, an estimated number of clock cycles required for each operation may be computed. The estimated number of clock cycles per operation is then multiplied by the number of operations per n and the expected number of n. This result is the expected number of CPU clock cycles for the problem size n, which may then be divided by the clock frequency to achieve an estimate of the CPU time required.
A similar method derives an estimate of the memory intensity. Here, the constants behind the asymptotic bound of space complexity, which are often omitted with big-O notation, are useful. These constants together with the bound give an estimate of the space complexity in terms of n. Examining the code will then determine the amount of memory bytes read and written for each n. Multiplying these terms provides the expected bytes in terms of n. Plugging in the given problem size n and then dividing by the bus speed in terms of bytes per second will provide an estimate of the time spent reading and writing to memory. The compute intensity and memory intensity may then be compared to determine which is the bounding factor.
Returning to the previous example that computed Laplace's equation, based on the code we expected the primary portion of the application to be compute-intensive rather than memory-intensive. The following "back-of-the-envelope" calculations are derived in the step-by-step fashion described above.
Computational IntensityFollowing this example, the computational and memory intensity calculations support our earlier expectations. Because the computational intensity is about 1.4x greater than the memory intensity, this calculation supports the premise that this particular operation is compute-bound rather than memory-bound, given this particular problem size.
This subsection introduced analytical techniques for determining computational and memory intensity in the context of multi-core CPU performance. The step-by-step technique assists in producing estimates that indicate whether a particular operation is compute-bound or memory-bound, which will assist in further analysis or optimization.
This section introduced analytical modeling techniques that assist in quantifying multi-core processor performance. Amdahl's law makes predictions about potential speedup through parallelization given a particular ratio of serial to parallel work. Gustafson's law changes assumptions to produce a more optimistic model for highly parallelized workloads with large data sets. Finally, the computational and memory intensity techniques assist the analyst in identifying compute-bound versus memory-bound operations.
In this paper the goal was to provide an overview of multi-core processor characteristics, performance behavior, measurement tools, and analytical modeling tools to conduct performance analysis. Because understanding the behavior and architecture of a multi-core processor is necessary to proficiently analyze its performance, the first section defined a multi-core processor in general terms, then introduced the primary types of multi-core processors used in computing—CPUs, GPUs, and FPGAs. The first section then compared CPUs and GPUs for their relative performance strengths, and subsequently the focus was narrowed to multi-core CPUs. The second section introduced three types of parallelism that impact multi-core processor performance: instruction-level parallelism, thread-level parallelism, and data-level parallelism. Each technique has potential performance benefits and detriments, and in-depth analysis of the underlying processor architecture, thread performance factors, and data coherence performance factors will lead to improved analysis. The third section discussed profiling and benchmarking tools that assist the analyst in measuring performance of a multi-core CPU. This section also introduced an example program that solves Laplace's equation; this program's performance measurement results were then reviewed for insights. The fourth section introduced analytical modeling techniques that assist in quantifying multi-core processor performance. This section compared Amdahl's predictions about serial versus parallel performance scaling with Gustafson's predictions and with the performance of the example application. Lastly, the fourth section introduced techniques to estimate computational and memory intensity and provided calculations using the example problem for illustration. In summary, as the analyst's knowledge of the particular characteristics of multi-core CPU architecture increases, the utility of the performance analysis can only increase as well.