| Son Dinh, sonndinh (at) go.wustl.edu (A paper written under the guidance of Prof. Raj Jain) |
Download |
Keywords: spin locks, mutual exclusion, synchronization, parallel computing, priority inversion, priority inheritance, priority ceiling, real-time parallel tasks
Real-time systems can be found anywhere today, from non-critical systems like real-time data streaming to safety-critical systems like automotive anti-lock braking system or avionics autopilot system. In these systems, critical tasks must be guaranteed to meet deadline. Otherwise, the consequence could be catastrophic. A typical real-time system consists of a set of real-time tasks running on a computer system, each characterized by relative deadline, execution time, and period. A real-time task set is called schedulable if all tasks in the task set are schedulable, which means all tasks meet their deadlines. Besides, tasks in a task set can share a set of resources, in which each requires sequential accesses. Resource contentions increase tasks' finishing time and thus affect the schedulability of the task set. Therefore, it is important to understand how synchronization of resource sharing affects the performance of a real-time task set.
Regarding the subject of synchronization in real-time systems, researchers have been analyzing and designing synchronization protocols to coordinate accesses to shared resources between different tasks. However, all of the existing works have focused on sequential tasks, where each task in the task set is executed sequentially, and there is no known work involving synchronization between parallel tasks, where each task runs in parallel. In this paper, we would like to investigate the blocking time that a real-time parallel task might incur because of resource contentions.
In order to enforce sequential accesses on resources, we utilize a popular strategy of mutual exclusion, named spin locks. The remaining of this paper is organized as follows. Section 2 discusses a fundamental problem with resource sharing in real-time systems, and how it is avoided in sequential task sets, as well as a new challenge that is posed in parallel task model. Section 3 talks about our method for analyzing the blocking time bound for parallel tasks. Section 4 proposes an experimental design to compare two types of spin locks and our expected results. Section 5 summarizes the paper and a lesson learnt.
In order to understand the challenge of analyzing blocking time for real-time parallel tasks, we first discuss the classic problem inherent to synchronization in real-time systems. Then we will look at the task model for parallel task set and a recent scheduler for this task model. Finally, we discuss why estimating blocking time in a real-time parallel task set is different than that for a sequential task set.
As mentioned before, a typical real-time system consists of a set of real-time tasks running on a computer system. Each task in the system often consists of an infinite sequence of periodic jobs; where the inter-arrival between two consecutive jobs is called period of the task. Thus, a task is characterized by several parameters including period, worst-case execution time (WCET), and relative deadline. As the names suggest, a task's WCET is the upper bound of the execution time of the task measured on a computer system it runs on; a task's relative deadline is the duration of time since the release time, a job of that task must finish to meet its deadline. Each task also has a priority to reflect the importance of the task and indicate the order in which tasks are scheduled: a higher priority task can preempt a lower priority task. Typically, a real-time task is of higher important and critical if missing its deadline causes severe consequences on the system. Therefore, a more important task should be assigned higher priority than a less important one.
Historically, when a typical computer system was equipped with a uniprocessor, a task set consists of sequential tasks and they share access to a set of resources. Each shared resource is protected by a lock. A task must acquire the resource's lock before accessing to a resource (entering its critical section), and must release the lock as soon as it finishes with the resource (exiting its critical section). While a resource's lock is being held by a task, other tasks trying to acquire the lock of the same resource must wait until the current resource-occupying task release the resource's lock. Generally, that mutual exclusion requirement can be done by either suspension, in which waiting tasks suspend and yield processor or spinning, in which waiting tasks spin (repeatedly check for the resource). In a uniprocessor system, spin waiting makes no sense because if a task spins, the system simply makes no progress other than one task spinning. Thus, suspension is an obvious choice in uniprocessor system.
However, synchronization of real-time tasks in uniprocessor system has a classic problem, called priority inversion. Figure 1 demonstrates this problem.
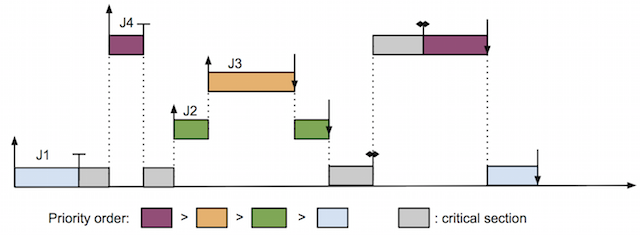
In this example, there are 4 tasks in the task set, all running on a uniprocessor. For the sake of simplicity, we drew only 1 job for each task: J1, J2, J3, J4 are a job of task 1, task 2, task 3, task 4, respectively. Job J1 has lowest priority. Job J4 has highest priority. Job J2 and J3 have priorities in between and J2 has lower priority than J3. The figure depicts events occur in time while these tasks are scheduled. The priority inversion problem happens when a higher priority job must wait for lower priority jobs (might be more than 1 such job), which is unacceptable in real-time systems since it causes higher priority job to miss its deadline. In this example, jobs J1 and J4 share a resource, named resource 1. Jobs J2 and J3 do not share any resource with other jobs. In the context of synchronization, the duration from the time a job acquire a resource to the time it releases that resource is called critical section. Since accesses to the same resource must be synchronized, critical sections access to a resource must be serialized; which means they must execute one after another and cannot execute simultaneously.
In this figure, the critical sections of J1 and J4 are denoted by gray boxes. Job J1 acquires resource 1 first and executes its critical section. Then J4 arrives; and because J4 has highest priority, it preempts J1 and executes until the time when it tries to acquire access to resource 1 too. However, resource 1 is already held by J1, J4 must wait until J1 releases resource 1. Unfortunately, while J1 executes its critical section, J2 arrives. J2 has higher priority than J1, thus it preempts J1 and executes. Even worse, J3 arrives and preempts J2 while it is running. This lengthens the duration that J1 is preempted and delays the time J1 releases the resource. As a result, J4, the highest priority job must wait for lower priority jobs include all J1, J2, and J3, just like if J1, J2, J3 had higher priorities than J4's. Priority inversion can affect J4 severely if the number of intermediate-priority jobs arrives and preempts J1 inside its critical section is large. Since it unnecessarily delays the completion time of J4, the highest priority job, we would like to avoid this problem.
As a real world example, in 1997, a Mars Pathfinder spacecraft (figure 2) has encountered priority inversion problem while roving on Mars surface. It was later discovered that a critical task of the spacecraft was blocked by lower priority tasks in a similar pattern as in previous example. This caused the critical task missed deadline and hence forced the computer system of the spacecraft to be reset [Mars97].
A popular method to overcome priority inversion is priority inheritance protocol [Lui90], in which a lower priority job holding resource inherits priority of a higher priority job trying to acquire the same resource. Figure 3 demonstrates this solution.
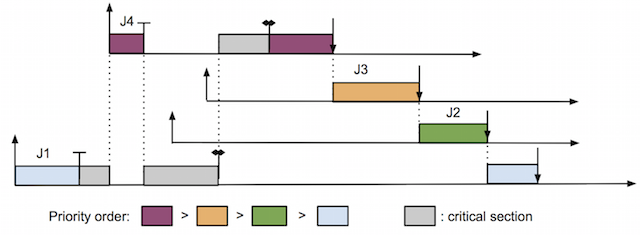
In this protocol, when J4 tries to acquire resource 1 and fails as it is already held by J1, J1 inherits J4's priority and becomes the highest priority job. Therefore, it cannot be preempted by J2 and J3 while executing its critical section. As soon as J1 releases resource 1, its priority reverts to the original value. At the same time, J4 can now acquire resource 1 and execute until it finishes. Thus, the delay of J4 is bounded by the duration of the critical section of J1; which is much better than without priority inheritance protocol. However, priority inheritance protocol still has drawbacks such as it cannot avoid deadlock, which could be solved with more advanced protocols like priority ceiling protocol [Lui90]. Equivalently, stack-based resource policy can be used as an alternative to priority ceiling protocol [Baker91]. Having discussed about synchronization of real-time systems in uniprocessor, we now move to synchronization in multiprocessor platform.
With the advent of chip-multiprocessors, many researches in real-time systems have been focused on new scheduling algorithms as well as synchronization protocols to coordinate tasks. In most of the works, real-time task set model keeps the same as in uniprocessor system; i.e., it consists of a set of sequential real-time tasks characterized by periods, WCETs, and relative deadlines. As before, the task set may have a set of shared resources, in which multiple tasks can access to the same resource. However, in contrast to uniprocessor systems where all tasks are scheduled on a single processor, in multiprocessor systems, tasks can execute simultaneously on different processors. Regarding scheduling algorithms for real-time tasks on multiprocessor systems, there are two main strategies: partitioned scheduling and global scheduling. In partitioned scheduling, tasks in a task set are assigned to processors and once a task is assigned to a processor, it cannot be migrated to another processor. In global scheduling, there is no strict association of a task with any processor, i.e., a task can be migrated to and executed on any processor that fits its computing demand.
The difference in the way tasks are scheduled leads to a new challenge of synchronization of resource sharing among tasks. Consider a task set of three tasks T1, T2, and T3 sorted in decreasing order of priority. Tasks T1 and T2 are assigned to processor P1. Task T3 is assigned to processor P2. Tasks T2 and T3 share a resource 1. Suppose that when a job J3 of task T3 tries to acquire resource 1, the resource is already locked by a job J2 of task T2. Thus, J3 must wait (either by spinning or suspending). While J2 executes its critical section, a job J1 of task T1 arrives and preempts J2. Because of that, J3 now must wait not only for J2 to release resource 1 but also for J1 to finish its whole execution (so that J2 can execute the remaining part of its critical section). This happens even though J1 does not share resource 1 with J3. Moreover, there may be multiple higher priority tasks executing in the same processor as J2 and if they arrive during the interval of J2's critical section, J3 might be blocked for extremely long. In multiprocessor real-time systems, J3 is said to be remote blocked, and we would like to limit the amount of remote blocking a job might incur.
Directly applying synchronization protocols for uniprocessor systems to multiprocessor systems is not enough. Therefore, researches have been focused on designing new protocols for coordinating shared resources in multiprocessor real-time systems. The two first protocols proposed for multiprocessor platform are distributed priority ceiling protocol and multiprocessor priority ceiling protocol [Rajkumar88][Rajkumar90]. In these papers, the authors had extended the priority ceiling protocol to the context of multiprocessors, where the first one was designed to work in distributed multiprocessor systems (non-shared memory) and the second one was targeted to shared memory multiprocessor systems. Even though the first protocols have appeared since 90s, design and analysis synchronization protocols for multiprocessor real-time systems are still active. Recent works in this topic introduced new protocols with improved blocking time bound for tasks [Block07][Brandenburg10][BrandenburgAn08][BrandenburgCa08][Gai03].
So far, we have been discussing about real-time systems composed of sequential tasks. However, there exist high computation demand real-time applications, which require to be executed in parallel to meet their timing constraints. This is when real-time parallel tasks model comes into play. In the next section, we will examine a real-time parallel task model.
A real-time parallel task set consists of a set of parallel tasks in which each task is typically a multithreaded program and executes on multiple processors. A parallel task is modeled as a directed acyclic graph (DAG). Each node in the graph represents a strand, which is a sequential execution of a set of instructions. Arrows represent the dependences between nodes in a graph. A node can execute only after all its dependencies have finished. Figure 4 presents an example of the DAG structure of a task.
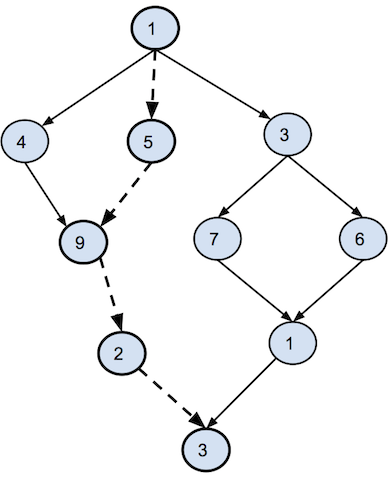
The number inside each note denotes the length of that node. Its unit could be number of instructions or time duration to run that node. A critical path of a parallel task is a longest path from the source node (the uppermost node in this example) to the sink node (the bottommost node in this example) of the DAG of that task. In other words, it is the time to finish the execution of that task given infinite number of processors. In this example, the critical path is represented by bold nodes and dashed arrows between nodes, and the length of this path is 20.
Recently, a new scheduling algorithm was devised to schedule real-time parallel tasks [Li14]. The basic idea of the algorithm is to allocate a set of designated processors for each task and execute it in parallel on the allocated processors. In this algorithm, each task Ti is allocated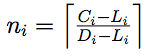 
processors; where Ci, Li, Di are the task's WCET, critical path length, and relative deadline, respectively. The algorithm guarantees that with ni processors, task Ti will meet its deadline. As before, parallel tasks access to a set of shared resources and multiple tasks might share the same resource. Each resource is protected by a spinlock, i.e., waiting tasks must spinning-wait for the resource. It is practical especially when critical sections are short compared to the cost of switching context among tasks. Actually, AUTOSAR (AUTomotive Open System ARchitecture), an open and standardized automotive software architecture, has mandated the use of spin locks in its architecture [Autosar].
Having discussed about some background of real-time systems studies, in the next section, we will examine briefly a method to analyze the worst case blocking time that a parallel task might incur because of resource contentions.
There is a fundamental difference between blocking analysis of sequential tasks and parallel tasks. With parallel tasks, a task contends for resource not only with other tasks but also with itself. This is possible because several threads of the same task might try to access a resource at the same time. Hence, we cannot directly use existing protocols designed for sequential tasks model to parallel tasks model. Figure 5 shows an example of schedule of parallel tasks with a shared resource, in which requests to resource are served in FIFO order.
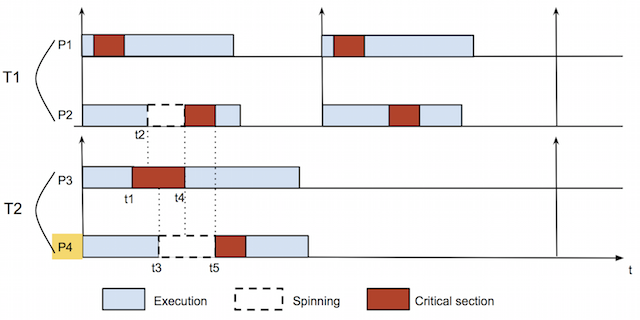
In this example, the task set consists of two parallel tasks, T1 and T2. Each task is assigned two processors: T1 executes on processors P1 and P2, T2 executes on processors P3 and P4. Blue boxes denote normal executions of tasks. Red boxes represent the executions of critical sections of tasks. Spin-waiting durations are denoted with dashed-border white boxes. Both tasks access to the same resource, named resource 1. The upward arrows at the beginning of tasks' executions indicate the arrival times of those tasks. In this example, there are three requests to resource 1 at times t1, t2, and t3. At time t1, task T2 issues a request to resource 1 from its processor P3. Since it is the first one trying to access resource 1, it gets the lock of resource 1 and then runs its critical section. Later at time t2, T1 also tries to access resource 1 with a request sent from processor P2. However, it must wait (by spinning) because resource 1's lock is being held by T2. Finally, at time t3, another request to resource 1 is sent from processor P4 of task T2. Similar to the previous request from T1, it must wait in resource's queue. As soon as T2 releases the lock at time t4, the request from P2 of task T1 acquires the lock and executes its critical section until time t5. At that time, the last request to resource 1 is satisfied.
As you might notice, the blocking time a task incurs depends not only on interferences from other tasks but also on request pattern of requests issued from its processors. Consider blocking time on processor P4 of task T2. In this example, it incurs a blocking duration equals to the sum of the critical section of P2 and a part of the critical section of P3, which is also a processor of T2. The difficulty of the problem of bounding the worst case blocking time on P4 lies on the fact that we do not know the distribution of the requests (to resource 1) of T2 over its processors: how many requests sent from P3? How many requests sent from P4? The only thing we know is the total number of requests (to resource 1) of T2.
In order to find the worst case blocking time of P4, we have formulated this problem as an optimization (more specifically, maximization) problem. For each request from T2 to resource 1, we use an indicator variable to indicate whether the request is issued from processor P4. We use another variable for each request to account for the fraction of the corresponding critical section will contribute to the blocking of P4. Then we impose constraints on those variables based on the serving order of spin locks (FIFO in figure 5) and build an objective function for the optimization problem. The worst case blocking time of P4 is then obtained by solving the optimization problem.
We would like to compare the worst case blocking time for two types of spin locks: FIFO-ordered and Priority-ordered. The FIFO-ordered spin locks simply serve requests in FIFO order, i.e., whichever request came first will receive the lock first. On the other hand, priority-ordered spin locks serve requests based on its priority, i.e., whichever request has highest priority will receive the lock first. Table 1 lists the set of factors of the experiment.
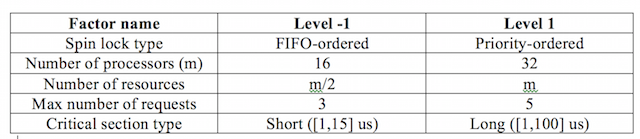
The first factor is the types of spin locks we are comparing. The number of processors (m) is the total number of processors in the systems. We consider two levels of this factor, 16 or 32 processors. The third factor is the total number of shared resources in the systems. Its values are chosen based on the number of processors m. There are 2 values we consider, m/2 or m resources. The next factor is the upper bound on the number of requests to a resource a job can access (Nmax). It could be 3 or 5, which means a job can access to a resource at most 3 or 5 times respectively. The last factor is critical section type. We consider two types of critical section length, short and long. A short critical section has length inside a range of [1, 15] microseconds and a long critical section has length in a range of [1, 100] microseconds. We randomly generate lengths for short and long critical sections in the corresponding ranges.
For each task in a task set, we generate its parameters as follows. The task's period is randomly generated in range of [10,1000] milliseconds. Note that we are considering implicit deadline task set, i.e., task's relative deadline equals to its period. Thus the generated period is also the relative deadline (D) of the task. The critical path length (L) of the task is generated randomly from 1 millisecond to D/3. Task's utilization (U), which is a fraction of its WCET and period, is chosen randomly in the range of (1, sqrt(m)/3], where sqrt(m) is the square root of the number of processors. Since utilization of a task U=C/T, we can easily calculate the worst-case execution time C of the task. To generate a task set, we keep adding tasks to the task set as long as the total utilization of the task set is still less than m/2 [Li14].
For each shared resource, we decide the number of tasks sharing that resource, which is relative to the total number of tasks in the task set. Tasks accessing this resource are chosen randomly and we keep adding tasks to the set of tasks sharing the resource until it reaches the number decided in previous step. Finally, the number of requests to a resource a task sends is picked randomly from 1 to Nmax.
As discussed in section 3, the metric of the experiment is the upper bound of the blocking time a task may incur. This is a lower-is-better metric (LB) since a task spending less time on spinning has better chance of meeting its deadline. We design the experiment using a 2k*r factorial design. For each combination of factors' levels, the experiment is replicated 10 times. We use IBM ILOG Cplex optimizer [Cplex] to solve the maximization problem of the worst case blocking time. The worst case blocking time is then used to compare FIFO-ordered and priority-ordered spin locks.
While the work is still in progress and we are still working on gathering data for the experiment, we expect that the priority-ordered spin locks would be preferable for higher priority tasks since they do not have to wait for lower priority tasks while accessing to shared resources. However, priority-ordered spin locks can starve lower priority tasks if higher priority tasks constantly issue requests. FIFO-ordered spin locks provide fairness among tasks at a cost of probably longer blocking time for higher priority tasks.
In this paper, we have discussed the fundamental problem of synchronization in real-time systems and seen why it is important to have a well-designed synchronization protocol to avoid the priority inversion problem. We have also examined new trends in multiprocessor real-time systems and observed the lack of work in the topic of synchronization of real-time parallel tasks. Unlike sequential tasks, synchronization of parallel task has an inherent difficulty in which threads of the same task can contend for shared resources with itself.
The proposed method for analyzing the worst case blocking time of real-time parallel tasks has been discussed. The basic idea is to formulate the problem of bounding the worst case blocking time as an optimization problem and utilize an existing optimizer like IBM Cplex to solve it. We believe that it is a more systematic approach for this problem than the existing methods and hence can be extended to analyze new synchronization protocols.
We have also discussed the experiment design for comparing two types of spin locks using a full factor with replication design. Even though the experiment have not been done yet and we cannot conclude which type of spin locks is better at this stage of the work, we have already learnt an interesting lesson on experimental design of problem with mixed categorical and continuous factors. That is we can treat a continuous factor as a categorical factor with some representative levels. A good choice of representative levels would reduce the time to conduct the experiment while still retains the precise of the results.
[Lui90] Lui Sha, Rajkumar, R., Lehoczky, J.P. “Priority inheritance protocols: an approach to real-time synchronization”. IEEE Transactions on Computers 39(9), 1175-1185. http://dl.acm.org/citation.cfm?id=626613
[Baker91] Baker, Theodore P. (1991). “Stack-based scheduling of realtime processes”. Real-Time Systems 3(1), 67-99. http://link.springer.com/article/10.1007/BF00365393
[Block07] Block, A., Leontyev, H., Brandenburg, B.B., Anderson, J.H. (2007). “A flexible real-time locking protocol for multiprocessors”. 13th IEEE International Conference on Embedded and Real-Time Computing Systems and Applications (pp. 47-56). http://dl.acm.org/citation.cfm?id=1307316
[Rajkumar88] Rajkumar, R., Lui Sha, Lehoczky, J.P. “Real-time synchronization protocols for multiprocessors”. In proceedings of Real-Time Systems Symposium, 1988., pp. 259-269. /">http://ieeexplore.ieee.org/document/51121
[Rajkumar90] Rajkumar, R. “Real-time synchronization protocols for shared memory multiprocessors”. In proceedings of 10th International Conference on Distributed Computing Systems, 1990, pp. 116-123. /">http://ieeexplore.ieee.org/document/89257
[Brandenburg10] Brandenburg, B.B., Anderson, J.H. “Optimality results for multiprocessor real-time locking”. IEEE 31st Real-Time Systems Symposium, pp. 49-60. http://dl.acm.org/citation.cfm?id=1936220
[BrandenburgAn08] Brandenburg, B.B, Anderson, J.H. “An implementation of the PCP, SRP, D-PCP, M-PCP, and FMLP Real-time synchronization protocols in LITMUS^RT”. 14th IEEE International Conference on Embedded and Real-Time Computing Systems and Applications, 2008, pp. 185-194. http://dl.acm.org/citation.cfm?id=1438559
[Gai03] Gai, P., Di Natale, M., Lipari, G., Ferrari, A., Gabellini, C., Marceca, P. “A comparison of MPCP and MSRP when sharing resources in the Janus multiple-processor on a chip platform”. Real-Time and Embedded Technology and Applications Symposium, 2003, pp. 189-198. http://dl.acm.org/citation.cfm?id=828537
[BrandenburgCa08] Brandenburg, B.B, Calandrino, J.M, Block, A, Leontyev, H., Anderson, J.H. “Real-time synchronization on multiprocessors: To block or Not to block, to Suspend or Spin?”. Real-Time and Embedded Technology and Applications Symposium, 2008, pp. 342-353.http://dl.acm.org/citation.cfm?id=1440601
[Li14] Jing Li, Jian Jia Chen, Agrawal, K., Chenyang Lu, Gill, C., Saifullah, A. “Analysis of federated and global scheduling for parallel real-time tasks”. 26th Euromicro Conference on Real-Time Systems, 2014, pp. 85-96. http://ieeexplore.ieee.org/document/6932592/
AUTOSAR standardized automotive architecture. http://www.autosar.org/
[Cplex] IBM Cplex optimizer. http://www-01.ibm.com/software/commerce/optimization/cplex-optimizer/
[Mars97] What really happened on Mars? http://research.microsoft.com/en-us/um/people/mbj/Mars_Pathfinder/Authoritative_Account.html
