Quantum cryptography is an emerging technology in the field of cryptographic systems where quantum mechanics is used to guarantee secure communication between two parties. In simple terms, quantum cryptography uses the principles of quantum mechanics to provide communication between two parties where eavesdropping can be detected by both the sender and the receiver. The first commercial application is applied towards securing electronic ballots. This paper will discuss what is needed to make electronic ballots secure, how quantum cryptography is used to make electronic ballots secure, the principles that make quantum cryptography secure and the quantum key distribution protocols used to perform quantum key distribution. This paper will also discuss the flaws of quantum cryptographic systems along with the plans for enhancing current quantum cryptographic systems.
Quantum Cryptography, cryptography, secure ballots, electronic ballots, electronic voting, quantum key distribution, BB84 encoding scheme, B92 encoding scheme, Ekert encoding scheme, information reconciliation, privacy amplification, Heisenberg’s uncertainty principle, denial of service, man-in-the-middle.
Quantum cryptography is an emerging technology in the field of cryptographic systems where quantum mechanics is used to guarantee secure communication between two parties. Quantum cryptographic systems seem to offer an unbreakable way to secure communication in a way that eavesdropping by a third party is detectable, if you can understand the quantum mechanics ensuring this guarantee, such as Heisenberg's Uncertainty Principle and quantum entanglement.QC systems encode information in the quantum properties of photons, using one of the three protocols discussed in later sections: BB83 encoding scheme, B92 encoding scheme or the Ekert encoding scheme.
Although quantum cryptography has great potential, it is not a good choice for encrypting and decrypting an entire conversation because of its range and payload limitations. As a result quantum cryptography’s primary function is for exchanging secret keys where an encryption method such as AES or triple-DES is used to encrypt and decrypt the rest of the conversation. Also, the quantum mechanic principles used are based on the single photons, but current QC implementations send bursts of protons, so additional methods are used to increase the level of security offered, such as information reconciliation and privacy amplification.
Currently, the Swiss community is using quantum cryptographic systems to secure electronic ballots in public elections, although quantum cryptographics is still considered experimental. Advances in this field are still being made along with ways to implement this technology in a wireless environment. As promising as quantum cryptographics may be, before it can be used to secure electronic ballots, one must know what makes electronic ballots secure.
Back to Table of ContentsThe basic quantum cryptography (QC) technology was originally developed by Charles Bennett, an IBM research staff member and IBM fellow, along with Giles Brassard of the University of Montreal in 1984. Their initially developed quantum cryptographic box was called BB84. The BB84 has been the basis for the majority of current implementations of quantum cryptographic systems. As implied in the name, quantum cryptographic technology uses quantum mechanics (specifically the Heisenberg Uncertainty Principle and Quantum Superposition or Quantum Entanglement). These fundamental quantum mechanic principles are used in combination with Privacy Amplification and Information Reconciliation to make quantum cryptography secure. Information exchange within a quantum cryptographic system consists of encoding information into protons in a way that interception or monitoring by a third party is detectable by the sender and recipient.
The major difference between QC technology and traditional cryptographic technology is that the QC relies on the laws of physics, specifically the laws of quantum mechanics, to provide a secure system, while traditional cryptographic systems rely on the computational difficulty of the encryption methods employed to provide a secure system. The laws of quantum physics make QC secure because of the following principles [Llp07].
Quantum key distribution (QKD) involves observing quantum states, where photons are put in a particular state by the sender and observed by the recipient. There are two different approaches to creating a quantum cryptographic system, polarized photons and entangled photons. This two approaches result in three different types of quantum cryptographic encoding protocols: BB84, B92 and the Ekert scheme.
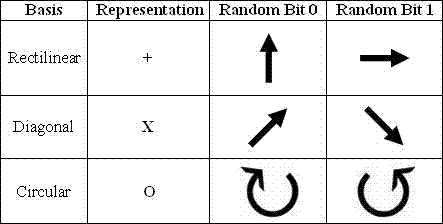
The typical way of encoding quantum information is by transmission of photons in some polarization states [Unk01]. Photon polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave [Jones06]. Polarization in general, is the property of electromagnetic waves describing the direction of oscillation in the plane perpendicular to the direction of travel. The protocol developed using polarized photons, known as BB84, was developed by Charles Bennett and Giles Brassard, uses Heisenberg’s Uncertainty Principle. The Heisenberg’s Uncertainty Principle states that it’s possible to encode information into the quantum properties of any substance particle in a way that any attempt to measure or monitor them would also disturb them in a detectable manner. In other words, information can be encoding into the quantum properties a particle, such as a photon, such that when the particle is measured, the quantum state of that particle will change in a detectable way. As stated before, in QKD, photons are placed into a particular state by the sender and observed by the recipient. Using Heisenberg’s Uncertainty Principle, certain quantum information cannot be measured or observed at the same time [Ford96]. These pieces of quantum information that cannot be measured simultaneously are called conjugates, which are complimentary properties on a quantum photon. In polarization, these conjugates are expressed in three different bases, rectilinear, circular, and diagonal. Observing one these bases will randomize all other conjugates so the sender and the receiver must agree on the basis of the quantum system they will be using, otherwise the receiver may accidentally destroy the sender’s information before using it.
The security of the BB84 protocol comes from encoding the quantum information in non-orthogonal states, where BB84 uses two pairs of states with each pair conjugate to the other and the two within a pair being orthogonal to each other. The typical polarization state pairs used are rectilinear basis of vertical (0°) and horizontal (90°), the diagonal basis of 45° and 135° or the circular basis of left- and right-handed. All three of these bases are conjugate to each other, so any two can be used together. The typical polarization state pairs are shown below in Table 1. The BB84 protocol uses the rectilinear and diagonal states.

When encoding with the BB84 protocol, Alice (the sender), creates a random bit 0 or 1 and then randomly selects one her two bases to transmit it in. She then creates a polarization state depending on both the random bit value chosen and the basis chosen. She then transmits a single photon to Bob, the receiver. The process is then repeated with Alice recording the state, basis and time of each photon sent. Bob does not know the basis the photons sent by Alice were encoded in so he selects a random basis to measure each photon, either rectilinear or diagonal. For each photon that Bob receives, he records the time and measurement basis used. After the photon transmission has ended, Alice broadcasts the basis used for each photon while Bob broadcasts the basis used to measure each photon. Both Alice and Bob discard the photons where Bob used a different basis for measurement then Alice used for encoding, which is half on average. The remaining bits are used as a shared key to encrypt and decrypt their conversation using some other cryptographic algorithm.
As stated before, this quantum encoding scheme is the basis for the majority of quantum cryptographic systems being researched and developed today, but a quantum cryptographic can be developed by using other encoding schemes such as B92 and the Ekert Scheme. The B92 quantum encoding scheme is similar to the BB84 quantum encoding scheme, but is considered easier to use.
The B92 encoding scheme was developed by Charles Bennett in 1992. This quantum encoding protocol is similar to the BB84, but uses only two of the four BB84 states, 0o and 45o to represent 0 and 1 [Llp07]. Using B92, Alice would encode her bits in two non-orthogonal BB84 states in a way that no one can determine a bit with certainty, because no measurement can distinguish between two non-orthogonal quantum states.
The security of the BB84 protocol comes from encoding the quantum information in non-orthogonal states, where BB84 uses two pairs of states with each pair conjugate to the other and the two within a pair being orthogonal to each other. The typical polarization state pairs used are rectilinear basis of vertical (0°) and horizontal (90°), the diagonal basis of 45° and 135° or the circular basis of left- and right-handed. All three of these bases are conjugate to each other, so any two can be used together. The typical polarization state pairs are shown below in Table 1. The BB84 protocol uses the rectilinear and diagonal states. Another encoding scheme that’s gaining popularity is called the Ekert encoding scheme. This encoding scheme is similar to BB84, but is based on two photons, called entangled photons.
The Ekert Scheme was developed by Arthur Ekert in 1991, which uses entangled pairs of photons. These photon pairs can be created by either Alice, Bob or a third party. These pairs are created by splitting a single photon into two, using a laser. After the split, one of the photons is sent by the sender or on behalf of the sender to the receiver while the other photon is kept. The entangled photons follow a principle similar the Heisenberg’s Uncertainty Principle where disturbing, monitoring or measuring, the state of one entangled photon will disturb the other entangled photon no matter how far apart the entangled paired photons are separated [Knight04]. The Ekert encoding scheme is set up similar to the BB84 protocol where four different polarization states are used.
When Encoding with the Ekert Scheme, Alice (the sender), creates a random bit 0 or 1 and randomly selects one of the three bases to transmit it in. She then creates an EPR pair in the selected state. An EPR pair is a pair of photons that follows the EPR paradox, which states that if one takes quantum mechanics and adds some reasonable conditions, such as locality, then one obtains contradiction [Derkson01]. In simpler words, the EPR paradox illustrates how quantum mechanics violates classical intuitions. Alice keeps one of the photons and transmits the other to Bob. Alice and Bob then randomly select a basis to measure each received photon. Alice records her measurements and Bob records his measurements. The process is then repeated until a sufficient amount of photons are transmitted. Once the transmission has ended, both Alice and Bob discuss over a public channel which measurement basis they used for each photon. The two parties then separate the bits of the transmission into two groups called raw key and rejected key [Lomonaco98]. The raw key group contains the bits where Alice and Bob used the same basis for measurement. The rejected key group contains all the other bits. Now, Alice and Bob compare over a public channel their respective rejected key. If their comparison satisfies Bell’s inequality then a third party has been detected, then the entire process is repeated. Otherwise the raw key is retained.
As discussed in the above sections, third party monitoring can be detected, but a hacker can also gain information from the open discussion conducted by the sender and the receiver. Also, the process of detecting a third party is based on identifying the errors within the photons. To resolve this issue information reconciliation and privacy amplification are used. These processes reduce the amount of error in the photons, thereby increasing the number of bits that can be used for a shared secret key and reduce the amount of information that a third arty may have obtained.
The quantum cryptography protocols described above provide two parties with nearly identical secret keys along with an estimate of the discrepancy between the shared key. In quantum cryptographic systems, the discrepancy between the shared secret key can be due to either a third party eavesdropping or imperfections in the transmission line and/or equipment. For security purposes, the discrepancy is always assumed to be from third party eavesdropping, since there is no way to distinguish the true cause of the discrepancy.
Using the BB84 encoding scheme, Alice and Bob check for eavesdropping by comparing a portion of their remaining bits that they would use for a shared secret key. If a third party were eavesdropping, errors would be introduced into Bob’s photon measurements. If a number of bits beyond a threshold differ, the derived key is discarded and the process QKD process is repeated [Unk01].
Using the B92 encoding scheme, Bob can determine if a third party was eavesdropping directly from the measurements of the photon. As stated in the previous section, if the measurement of the photon is greater than 1 then the receiver can be certain that no one was eavesdropping otherwise the photon is discarded [Unkn01].
Using the Ekert encoding scheme, Bob and Alice check for eavesdropping by comparing their rejected bits, called the rejected key. If their comparison satisfies Bell’s inequality, then a third party has been detected and the entire process is repeated. Otherwise the raw key is retained. Bell’s inequality is essentially a method for determining the probability that two bits do not match given the measurement basis used.
Given an error rate between the shared key, two processes can be used to reduce the erroneous bits and reduce a third party’s knowledge of the key to a negligibly small value. The two processes are privacy amplification and information reconciliation, which are used together.
Information reconciliation is a form of error correction done between two participating parties’ shared secret keys, to ensure their shared secret key is identical. This process is conducted over a public channel. Since this process is conducted publicly, the cascade protocol is used which minimizes the information sent about each key. The cascade protocol is a parity based and interactive error-correction algorithm, which is time consuming, but allows for saving more of the key’s bits.
The information reconciliation process is conducted in several rounds, with both keys divided into blocks in each round and the parity of each block is compared [Bartlett07]. If a difference in parity is discovered, then a binary search is conducted to find and correct the error. If an error is discovered in a block from a previous round that was corrected then another error is known to be in the block. The error is then found and corrected as before. The process is recursively done until all blocks have been compared, which constitutes a round. Then both the sender and the receiver randomly reorder their keys in same manner and begin a new round. After a predetermined number of rounds, both parties will have identical keys, but a third party could have gained additional information about the keys through the exchange of information from the information reconciliation process. Privacy Amplification is used in conjunction with information reconciliation to reduce the amount of information a third party may have gained.
Privacy Amplification is a method for reducing a third party’s partial information about the shared secret key between two parties, Alice and Bob. Privacy amplification is used to convert the realized secret key into a smaller length key through some hashing function chosen at random from a known set of hashing functions. The sender chooses the hash function and announces it over a public channel. As with most hashing functions, the universal hash function takes a binary string of length equal to the key and outputs a binary string of a shorter length. The amount at which the key is shortened is calculated from how much partial information a third party could have gained, which is assumed to come entirely from the information reconciliation process.
Information reconciliation and privacy amplification help reduce the amount of information that a third party may have obtained through the open discussion conducted by the sender and the receiver, but QC systems are still susceptible to a number of hacker attacks.
In theory, quantum cryptographic systems can ensure that a secure communication has not been intercepted. But in practice, cryptographic systems are still considered an area of advanced research and are susceptible to many hacker attacks. However, they are considered secure because of the amount of technical skill needed to perform these attacks. Quantum Cryptographic systems are also not capable of transmitting large amounts of data as a whole. Its primary application is in the distribution of secret keys for the use of encrypting and decrypting a conversation over a fiber-optic line, which absorb the photons after some time. In the cryptographic community, quantum cryptography is considered a potential replacement of the Diffie-Hellman key exchange algorithm. In addition to the limitations of QC systems, the technology is still susceptible to several hacker attacks.
QC systems are essentially susceptible to three types of attacks: a non-traditional man-in-the-middle attack (MITM), denial of service (DoS) attacks, and an attack proposed by Adi Shamir, the inventor of the RSA algorithm. The attack proposed by Adi Shamir applies to the polarization schemes discussed, BB84 and B92 quantum encoding schemes. Instead of Eve, the eavesdropper, attempting to read the photons sent by Alice, she sends a large pulse of light back to Alice in between Alice’s photon transmissions. Regardless of how black Alice’s transmitting equipment may be, some light will be reflected back to Eve where she can discover the polarization state of Alice’s polarizer because the reflected light will be polarized in the same manner. The other two types of attacks, DoS and MITM, can be performed in two ways.
As stated above, the DoS attack can be performed in two ways: by compromising the quantum cryptographic hardware or by introducing extra noise into the QC system. QC systems use fiber optic channels, so Eve the hacker could simply cut the lines or tamper with the fiber-optic lines. The fiber-optic channel could be made unusable by simply trying to tap into the line. The QC equipment itself could be compromised to generate photons at random that are not secure by using a random number generator.
The other way to perform a DoS attack against a QC system is to introduce noise into the system. Because eavesdropping and noise are indistinguishable, Eve the hacker, could somehow introduce noise into the QC system, causing Alice and Bob to discard a higher number of a photons [Ford96]. Also, if the additional noise is sustained, Alice and Bob may increase their error threshold to compensate for the noise making eavesdropping attempts more possible.
Man-in-the-middle (MITM) attacks can also be performed in two different ways. Traditional MITM attacks do not work on QC systems because of the principles of quantum mechanics. With traditional MITM attacks the attack, Eve, would intercept the transmitted messages and transmit a duplicate in its place. However this is impossible due to the fundamental nature of QC systems, although non-traditional MITM attacks are possible. The first, involves Eve pretending to be "Alice" to Bob and "Bob" to Alice. Eve would then perform QC with both Alice and Bob at the same time, obtaining two keys, one for Alice and one for Bob. Alice’s key would be used to decrypt a message from Alice then reencrypted by Bob’s key and vice versa. This type of attack is possible, but preventable by performing some type of identity authentication.
The second type of MITM attack comes from the method photons are transmitted. Because it is difficult to use a single photon for transmission in the real world, most QC systems use small bursts of coherent light instead. In theory, Eve may be able to split a single proton from the burst without being detected. Eve could then observe the retrieved photons until the basis used to create then is announced.
Although QC systems are susceptible to a number of attacks, QC is still considered very secure because it would take a very knowledgeable person to implement the attacks discussed, which is why they are used by the Swiss for securing public ballot elections.
Back to Table of ContentsAs technology advances, electronic voting is becoming more of a normal occurrence in general elections. There are two main types of electronic voting machines, optical scan machines and direct-recording electronic (DRE) machines. A voter casting a ballot using optical scan machines involve the following three steps.
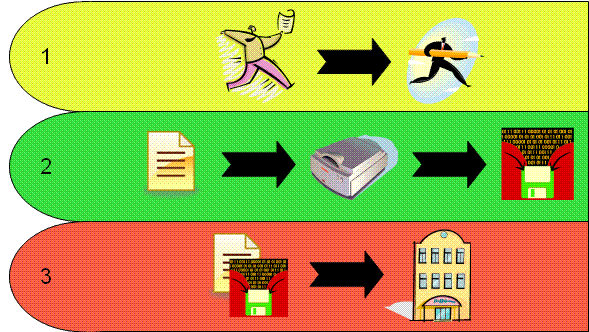
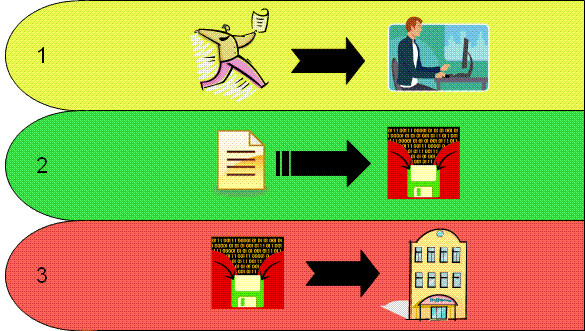
The three step process described for the optical scanning machines and DRE machines are susceptible to an attack at each step in the voting process. In step one of the voting processes; the machine could be compromised with vote stealing software. In this scenario, the voting machine needs to be physically secure to prevent against this type of attack. In step two of the voting process; the machine could be compromised to incorrectly record a vote where a person may be able to vote multiple times, delete votes, or disable the machine entirely. In this scenario, the voting machine needs to be physically secure in addition to a means of verifying a voter’s ballot was recorded correctly. In the third step in the voting process; the centralized tallying machine that performs the counting of the votes could be compromised, where the election could be skewed in any direction. In this scenario, the centralized voting machine needs to be physically secure and the transmission of votes from the voting machines needs to be secure as well.
The electronic voting process has a number of other vulnerabilities discovered by University of California researchers, but the vulnerabilities discussed cover a majority of them [Unk07]. As stated in the introduction, securing an electronic ballot is more than just protecting the electronic ballot against third party interception. The electronic voting systems must be physically secure as well as electronically secure. Quantum cryptographic systems only contribute to securing ballots at the third step of the voting process, specifically the electronic transmission of electronic ballots from one location to the centralized counting machine. This is how the technology is applied by the Swiss for securing electronic ballots during the parliamentary election held on October 21, 2007 [Messmer07].
Back to Table of ContentsGeneva, Switzerland has been the innovator of electronic voting by being one of the first to offer electronic voting over the internet. They have also been credited with being the first to use a quantum cryptographic system to secure electronic ballots over a fiber-optic line. The quantum cryptographic system was developed by Id Quantique in collaboration with Senetas by Professor Nicolas Gisin at the University of Geneva [Paul07]. The quantum cryptographic unit that was developed is called ID500. The price tag associated with this cryptographic box starts at $50,000 [Messmer04]. The technology has been in development for at least two decades and has benefited from financial support from the United States military.
The cryptographic systems employed by the Swiss are used for securing a link between the central ballot-counting station in downtown Geneva and government data centers in the suburbs of Geneva over fiber-optic channels. The newly used quantum cryptographic system is used to transmit the count totals of a public election. Quantum cryptographic technology is specifically used in the exchange of secret keys for point-to-point encryption methods such as Triple-DES or Advanced Encryption Standard at speeds of about 100 times a second and is capable of automatically detecting a third party from eavesdropping on the communication stream. The encryption boxes used by the Swiss use quantum cryptographic technology for exchanging secret keys and use Triple-DES to provide a secure point-to-point connection between two parties. Initially, the quantum cryptographic systems used by the Swiss proved to be successful, but they do have limitations, which include encryption speed and transmission distance. Currently, typical quantum cryptographic machines can only transmit at speeds of 100 Mbps while the Swiss system is capable of encrypting at 1 Gbps [Messmer04]. The hardware used is limited to a 50 mile transmission distance before the protons performing the encryption over the fiber-optic line begins to degrade. These limitations are introduced by how quantum cryptographic systems perform a key exchange.Currently, there are plans for enhancing QC systems to reduce these limitations and the amount susceptible attacks.
Back to Table of ContentsFuture enhancements of current QC systems include making QC more secure, increasing the transmission distance of fiber-optic lines, increasing encryption rates and making the technology wireless. One might think QC systems are unconditionally secure because of the quantum mechanics theory used, but the theory can only be solid if QC hardware transmits single photons. Current QC implementations do not transmit single protons, but bursts of protons. With photon bursts instead of single protons, eavesdropping attacks are possible because Eve could siphon off individual photons without being detected.
One proposal, introduced by Toshiba, for making QC systems more secure is by sending randomly interspersed pulses within the quantum signal called decoy pulses [Graham07]. These decoy pulses are of weakened strength than the real quantum signals, which means the decoy pulses rarely contain more than one photon. So, the sender and receiver can monitor the ratio of decoy pulses to real quantum singles that made it through to determine if an eavesdropper was present. With decoy pulses, Eve will have a harder time siphoning meaningful photons, decreasing the level of vulnerability of the QC system. This approach would also increase the transmission distance and encryption rate by 100-fold because stronger quantum pulses can be used.
Another advancement for making QC systems more secure is the development of a light emitting diode capable of emitting a single photon more reliably [Graham07]. Toshiba’s methodology is to create an array of quantum dots, each about 45 nanometers in diameter, for emitting a single photon. This advancement would increase the level of security offered by current QC systems, but does not resolve the transmission distance and encryption rate limitations. The most promising advancement to QC systems is the wireless application.
The theory discussed in this paper assumes that the quantum signals are transmitted across some medium, such as fiber-optics, or through free space. Current QC systems transmit their quantum signals across fiber-optic channels, but only a small few have been able to send quantum signals through free space. Current military plans are to use satellites to transmit quantum photons globally. Few people have been able to transmit QC photons through free space, but it has been proven that the wireless QC systems are conceivable. Having a wireless QC system would alleviate the transmission distance limitation. The encryption can be resolved with advancements of electronic hardware when larger capacity storage devices and better processors come available. Wireless QC systems are still in the development stage, but the few successful attempts are making strides in the realization of commercial wireless QC systems.
Back to Table of ContentsQuantum cryptographic systems are becoming more of a reality with each passing day. The primary use of QC systems is for the distribution of secret keys for encrypting and decrypting a conversation between two parties, but they are being used by several financial institutions and by the Swiss for securing electronic ballots and have been supported greatly by the military. The Swiss have successfully used quantum cryptographics in securing the ballots of a public election when the ballots are transferred from the voting centers to the counting and archiving center, which is only a portion of actually securing electronic ballots. Because QC systems are based off the principles of quantum mechanics, QC systems are inherently secure against eavesdropping, although QC systems are susceptible to several man-in-the-middle and denial of service attacks. There are several different ways to perform quantum key exchange, such as the BB84 protocol, the B92 protocol, and the Ekert scheme protocol. The QC system is very promising and advancements are being made to improve upon the technology, most notably a wireless implementation. With all the hype surrounding quantum cryptographic systems, the technology is very promising, but still susceptible to hacker attacks and has transmission distance and encryption rate limitations. These limitations are being addressed and proposals have been made to resolve these limitations and protect against the known hacker attacks, but it may be a while until the quantum cryptographic systems are accepted and used on a larger scale.
Back to Table of Contents[Bartlett07] Graeme Bartlett, "Quantum Cryptography", Wikipedia Article, November 2007, http://en.wikipedia.org/wiki/Quantum_cryptography. A Wikipedia Article discussing quantum cryptographics in general.
[Jones06] Roger D. Jones, "Photon Polarization", Wikipedia Article, August 2006, http://en.wikipedia.org/wiki/Photon_polarization. A Wikipedia Article discussing photon polarization.
[Knight04] Will Knight, "Entangled Photons Secure Money Transfer", New Scientist Article, April 2004, http://www.newscientist.com/article/dn4914-entangled-photons-secure-money-transfer.html. A New Scientist Article discussing the use entangled photons to secure money transfers.
[Messmer04] Ellen Messmer, "Quantum Crypto Coming to Light", Network World Article, April 2004, http://www.networkworld.com/newsletters/optical/2004/0419optical2.html. An article discussing the origins of quantum cryptography.
[Stokes06] Jon Stokes, "How to Steal an Election by Hacking the Vote", Network World Article, October 2006, http://arstechnica.com/articles/culture/evoting.ars. An article discussing how an election can be hacked.
[Messmer07] Ellen Messmer, "Quantum Cryptography to Secure Ballots in Swiss Election", Network World Article, October 2006, http://www.networkworld.com/news/2007/101007-quantum-cryptography-secure-ballots.html. An article discussing how the Swiss are using quantum cryptography towards securing ballots.
[Unk07] Unknown, "Potential Flaws in Electronic Voting Systems, Review Finds", Science Daily Article, 2007, http://www.sciencedaily.com/releases/2007/07/070730184838.htm. An article discussing the flaws of Internet voting.
[Paul07] Ryan Paul, "Geneva Brings Quantum Cryptography to Internet Voting", Ars Technica Article, 2007, http://arstechnica.com/news.ars/post/20071012-geneva-brings-quantum-cryptography-to-internet-voting.html. An article discussing how Geneva is applying quantum cryptography to Internet voting.
[Ford96] James Ford, "Quantum Cryptography Tutorial", Tutorial, 1996, http://www.cs.dartmouth.edu/~jford/crypto.html#3. A tutorial on quantum cryptographics.
[Unk01] Unknown, "The BB84 Quantum Coding Scheme", General Information, 2001, http://www.cki.au.dk/experiment/qrypto/doc/QuCrypt/bb84coding.html. A general discussion of the BB84 quantum encoding.
[Unkn01] Unknown, "The B92 Quantum Coding Scheme", General Information, 2001, http://www.cki.au.dk/experiment/qrypto/doc/QuCrypt/b92coding.html. A general discussion of the B92 quantum encoding.
[Llp07] Quantum Information Partners LLP, "Introduction to Quantum Cryptography", Quantum Information Partners Publications, 2007, http://www.qipartners.com/publications/Introduction_to_QC.pdf. A Wikipedia article discussing the EPR paradox.
[Derkson01] Bryan Derkson, "EPR Paradox", Wikipedia Article, 2001, http://en.wikipedia.org/wiki/EPR_paradox. An introduction to quantum cryptography.
[Lomonaco98] Samuel J. Lomonaco Jr, "A Quick Glance at Quantum Cryptography", Published Article, 1998, http://www.cs.umbc.edu/~lomonaco/lecturenotes/9811056.pdf. A published article on quantum cryptography.
[Graham07] Duncan Graham-Rowe, Foolproof Quantum Cryptography", Technology Review Article, 2007, http://www.technologyreview.com/Infotech/18253/?a=f. A published article on making quantum cryptography more secure..
[Kaufman02] Charlie Kaufman, Radia Perlman and Mike Speciner. Network Security: Private Communication in a Public World, 2nd Edition. Prentice Hall, 2002. ISBN 0130460192.
Back to Table of Contents| AES | Advanced Encryption Standard |
| B92 | Quantum key distribution scheme developed by Charles Bennett in 1992 |
| BB84 | Quantum key distribution scheme developed by Charles Bennett and Gilles Brassard in 1984 |
| BOE | Board of Elections |
| DES | Data Encryption Standard |
| DoS | Denial of Service Attack |
| DRE | Direct-recording Electronic Machines |
| EPR | Einstein-Podolsky-Rosen |
| IBM | International Business Machines Corporation |
| ID500 | Quantum cryptographic system developed by Id Quantique in collaboration with Senetas |
| MITM | Man-in-the-Middle attack |
| QKD | Quantum Key Distribution |
| QC | Quantum Cryptographics |
| RSA | A public key cryptography algorithm |
Last modified: December 2, 2007.
Note: This paper is available on-line at http://www.cse.wustl.edu/~jain/cse571-07/index.html