| Elom Worlanyo (A paper written under the guidance of Prof. Raj Jain) |
Download |
Network Coding (NC) is a relatively recent subset of network information theory that has led to great advancements in the optimization of network throughput. It involves performing operations other than mere forwarding and replication at the nodes that constitute a network. In this paper, we seek to review the developments in this field and examine the impact this has had on wireless networks, in terms of both the improvements it has made and its resulting application to various categories within wireless networking. We look at the theory behind NC, the various NC schemes that have been proposed and utilized over the years, the emergence of applying NC at the physical layer of networks, and various selected applications of NC in wireless networks.
Network Coding, Random Linear Coding, Opportunistic Coding, Triangular Coding, Butterfly Network, MAC-layer, P2P, Wireless Mesh Networks, Wireless Sensor Networks, Overlay Networks, Instant Messaging, Video on Demand, Multimedia
This paper seeks to explore the concept of network coding (NC), a relatively new subset of information theory, specifically within the domain of wireless networks. Prior to the seminal paper [Ahlswede00] describing this field, the transmission of data through a network was merely viewed as a commodity flow, which is an exchange of commodities without the ability to process the commodities themselves [Bassoli13]. Network coding changed that, suggesting that operations more complicated than simple replication and transmission of data packets could be performed at the nodes that make up a given network. This lead to rapid advancements and spurred the use of new mathematical tools, in fields such as algebra, matroid theory, geometry, graph theory, combinatorics and optimization theory among others [Bassoli13]. This resulted in network coding as it is today: a “broad and complex field rich in mathematical idiom” [Bassoli13].
While NC is a complicated topic to discuss without significant mathematical background, this paper is aimed towards a more casual audience and thus we will take steps to reduce the complexity of the mathematical theory discussed, while striving to still capture the various nuances within. In this introduction, we aim to give a succinct description of what NC entails, and in so doing shed light on the various characteristics defining this technology. In order to achieve this, we provide some background regarding NC and its underlying theory in this section, discuss popular coding schemes currently in use in Section II and briefly analyze physical layer-based network coding in Section III, focusing on physical network coding (PNC) since it is most used in wireless networks. We then look more closely at various applications of NC in wireless networks in Section IV, challenges faced by these applications in Section V and then conclude with a summary of the information we have obtained.
Network coding is a networking technique where operations, which in practice tend to be algebraic algorithms, are performed on data as it passes through the nodes within a network. While in theory any manner of algorithm could be performed on the data at a node, current NC algorithms tend to be concerned with accumulating the various transmissions that pass through a given node. In traditional routing networks, packets are simply cached and then forwarded to the next node downstream in the network. As such, if a routing node receives two packets from two distinct sources it will forward them sequentially, even if they are both addressed to the same destination, while queueing any others it may receive in the meantime. This results in the node creating separate transmissions for each and every message being delivered, which results in a decrease in network efficiency. NC is used to mitigate this by merging relevant messages at the relay node, using a given encoding, then forwarding this accumulated result to the destination for decoding. In order for this to work, the destination node needs to be synchronized with the transmitting nodes, a constraint especially important when it comes to network coding done at the physical layer [Liew13], which we shall discuss later on in Section III of this paper.
In [Ahlswede00], which defined the beginning of NC research, a multicast session over a directed graph with lossless links was considered. The results of this paper are expressed as the max-flow min-cut theorem in network theory. This theorem states that in a flow network, where information flows from one node to the next, the maximum amount of flow from the source to the sink (max-flow) is equal to the minimum capacity that would not allow any flow to pass from the source to sink when cut/removed from the network in a specific way (min-cut). [Ahlswede00] showed that when operations at intermediate nodes were allowed, the maximum multicast rate was equal to the minimum min-cut from the source to each receiver. Basically, if all receivers have the same min-cut from the source, then NC would allow all nodes to achieve the min-cut capacity simultaneously. This capacity would also correspond to the maximum flow rate that each receiver could get if it were the only receiving node in the network. The simplest example that demonstrates the key idea and the benefits of NC in the multicast case is the butterfly network depicted in Figure 1 .
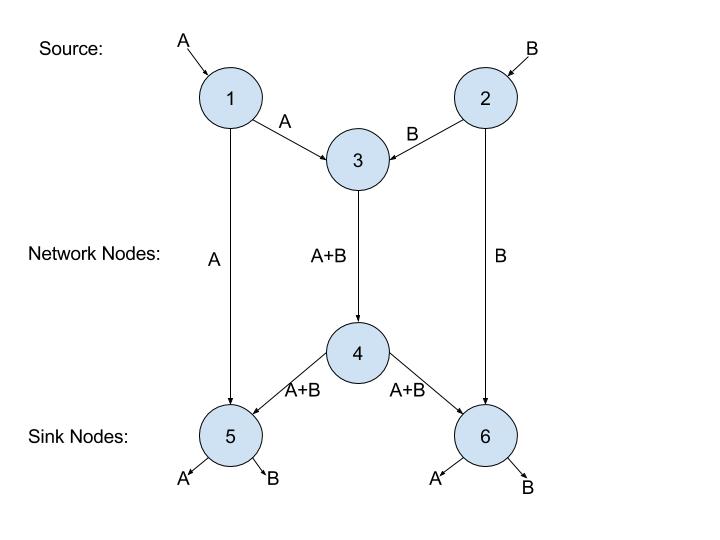
Figure 1: Butterfly Network [Magli13]
The two source nodes, nodes 1 and 2, have messages A and B respectively, that both need to be transmitted to the two destination/sink nodes, 5 and 6. Each edge in this network can only carry a single message. If nodes could only route/retransmit, then the central link would only be able to carry message A or message B, but not both of them at the same time. Assuming we sent message A through the central link between nodes 3 and 4, then node 5 would receive message A twice and would never receive message B. The same problem would occur at node 6 if we sent message B through the central link, with node 6 never receiving message A. We can immediately see here that routing would be insufficient to transmit both messages since no routing scheme can simultaneously transmit A and B to both sink nodes. This is where the operation on data at relay nodes come into play; a simple linear code is demonstrated here, where A and B are encoded using their sum. As such, in this example node 5 would receive both A and A+B, from which it can decode B by subtracting these two values. Node 6 would utilize the same procedure to decode A after receiving both B and A+B. From this simple example we can see that various other encoding techniques could be applied to a varying number of packets, in various network configurations. These techniques could greatly increase the amount of information that could be transmitted in a single instance, thus significantly improving the throughput and power efficiency of networks that implement them. This result can also be applied to wireless networks with two simultaneous unicast connections as shown below:
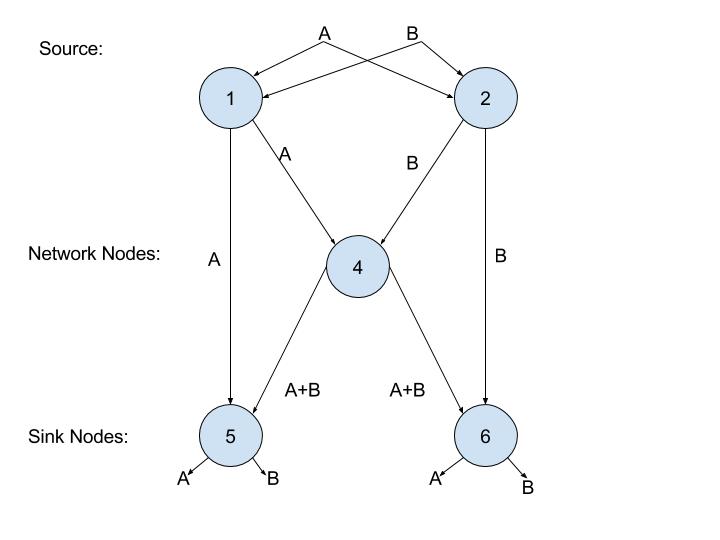
Figure 2: Modified wireless butterfly network [Magli13]
The modified wireless butterfly network shown in Figure 2 is different from the original butterfly network in the sense that packet transmissions can be transmitted from the source node to more than one node. Thus, transmissions are represented using hyper-arcs, instead of arcs.
We now have a brief and hopefully accessible overview of the theory behind, and the nature of network coding. In Section II we shall now look into some of the more popular coding schemes being utilized.
The manner in which nodes encode and decode the packets they transmit/receive can have a huge impact on the resulting throughput of the network. The majority of the NC schemes in use nowadays have their basis in algebraic theory. Whereas earlier schemes, such as the traditional XOR-coding scheme and the Deterministic Linear Network Coding scheme were deterministic in nature, the more common schemes in use today are non-deterministic, meaning they are free from the constraint of having packet feedback information for every transmitted packet from all the receivers. In this section we shall take a look at some common coding schemes, namely Random Linear Network Coding (RLNC), Triangular Network Coding (TNC) and Opportunistic Network Coding (ONC).
Here, we shall once again utilize a network model for a general communication system that consists of source, network and sink nodes connected by channels that are potentially lossy. We can represent such a system as a directed graph G = {V , E} where the vertices V represent the various nodes in the network and the set of edges E consists of arcs between nodes and denotes the links in the network [Magli13]. In RLNC, coded packets are random linear combinations of the original packets over a finite field of size q [Ostovari16]. Each coded packet is in the form:
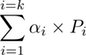
Here, αi and Ρi are random coefficients chosen from a Galois field and the packet respectively, while k is the number of packets that are coded together in that single transmission. A Galois field is any field that contains a finite number of elements. If the field size is large enough, the probability that the receiver(s) will obtain linearly independent combinations, approaches 100%. Linear independence is important in ensuring uniform distribution, thus reducing redundant information being forwarded to a given node. The smaller the field size, however, the less complex the resulting system, which is especially advantageous in wireless networks [Magli13]. Instead of transmitting the original packets, the source node generates and transmits random-coded packets over the k packets. In order to decode the coded packets and retrieve the original packets, the destination nodes need to receive k linearly independent coded packets. They can use Gaussian elimination to decode the coded packets [Ostovari16].
As powerful as this encoding scheme is, it does have its challenges, chief among them the fact that if a receiver gets an insufficient number of packets, it is extremely unlikely that it can recover any of the original packets. This is known as the index coding problem [Qureshi12]. This can be fixed by sending additional random linear combinations until the receiver receives the required number of packets. Other challenges include the high decoding computational complexity due to using the Gauss-Jordan elimination method and the high transmission overhead due adding large coefficient vectors to encoded blocks. Linear Network Coding (LNC) computational complexity makes it unsuitable for practical use in devices that operate on battery power, such as mobile phones and wireless sensors.
In order to intrinsically fix the problem with RLNC detailed above, where receivers that get an insufficient number of packets cannot recover the original packets, triangular network coding was proposed in [Qureshi12]. The triangular pattern based packet coding scheme is performed in two stages. First, redundant “0” bits are selectively added at the head and tail of each packet to make sure that all packets are of uniform bit length [Wiki1]. The packets are then XOR-coded bit by bit where the “0” bits are added in such a way that they generate a triangular pattern, known as triangularization, as shown in Figure 3.
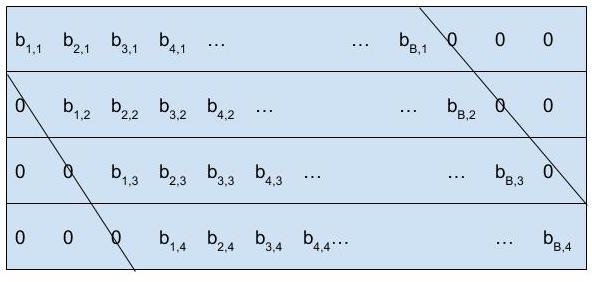
Figure 3: Triangular Pattern [Qureshi12]
The decoding process is similar to the LNC decoding process, which involves Gaussian elimination. However in this case, it is simplified since the coded packets are in a triangular pattern and as such the receiver only needs to perform back-substitution, where each row is solved, from the last row to the first row. This is far less computationally intense and gives triangular coding the bandwidth performance of LNC, while affording the computation cost of XOR coding [Qureshi12].
In ONC, the sensor nodes can snoop on all transmissions in their neighborhood and store the overheard data packets, whether they are intended for them or not [Shen12]. As such, the sensor nodes know the overheard and routed packets that each neighboring node possesses, and can perform network coding operations based on this information. Each node has its own queue of received uncoded packets p1,p2,...,pn whose destinations, determined by their packet headers and the node’s routing table, are r1,r2,...,rn. The node then dequeues the first packet, p1 and, while making sure all of next hop recipients can immediately decode the resulting combination, steps through the queue to greedily add packets for combination [Shen12]. A recipient can immediately decode a combined packet if it knows all but one uncoded packet. For example, a combined packet p1+p2+p3+p4 is valid if node r1 knows p3and p4, node r3 knows p1 and p4, and node r4 knows p1 and p3.
We are now familiar with some of the common coding schemes in use, and can now see that most of these are geared towards packet-based networks. In wireless networks however, there are significant gains to be made at layers beside the application layer, which is where the bulk of NC is done at present. We shall hence look at physical layer network coding in Section III.
Physical-layer network coding as a concept was proposed in 2006 for application in wireless networks [Liew13]. PNC’s main idea is to take advantage of the natural network coding operation that occurs when electromagnetic (EM) waves are superimposed on one another. This simple idea lead to numerous advancements, with subsequent works by various researchers leading to many new results in the domains of wireless communication, wireless information theory, and wireless networking. We shall attempt to give a brief overview of both the theory behind this concept and the implications of the results in the three fields listed above.
Interference is often treated as a destructive phenomenon in wireless communication networks today. When multiple transmitters send radio waves to their respective receivers, a receiver may receive signals from its transmitter as well as from other transmitters at the same time. The radio waves from the other transmitters are often treated as interference that corrupts the intended signal, as a result of their overlapping. In Wi-Fi networks, for example, when multiple nodes transmit together, packet collisions can occur leading to none of the packets being received correctly. PNC takes advantage of the fact that when multiple EM waves come together within the same physical space, they add together or superimpose, thus increasing in amplitude. This mixing of EM waves is a form of natural network coding, which is utilized in PNC [Liew13].
The concept of PNC can be most easily illustrated with a network model known as a Two-Way Relay Channel (TWRC). TWRC is a three-node linear network in which two end nodes, nodes T1 and T2, want to communicate via a relay node R. This is illustrated in Figure 4 below:
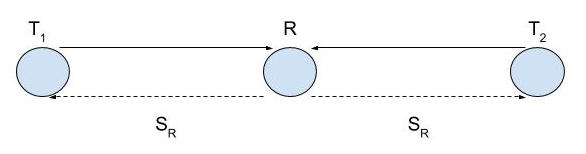
Figure 4: Two-Way Relay Channel [Liew13]
There is no direct signal path between nodes T1 and T2. A real-world example of such a system is a satellite network in which nodes T1 and T2 are the ground stations, and the relay R is the satellite. The half-duplex constraint is often imposed on wireless communication systems to ease engineering design [Liew13]. With the half-duplex constraint, a node cannot transmit and receive at the same time. The relay in TWRC thus cannot receive from node T1 or node T2 and transmit to them at the same time. This means that each packet from node T1 to node T2 (and similarly, each packet from node T2 to node T1) must use up at least two time slots to reach its destination. Thus, the best possible packet exchange throughput is two packets for every two slots, one in each direction.
We see that the use of natural network coding, through taking advantage of superimposition of waves could indeed be a major breakthrough. It is however subject to certain challenges we shall look at in the next subsection.
PNC can potentially achieve 100% and 50% throughput increases compared with traditional transmission and straightforward network coding, respectively, in multi-hop networks [Lu12]. PNC achieves this doubling of the TWRC throughput by reducing the needed time slots for the exchange of one packet from four to two [Lu12]. Unfortunately, PNC is yet to be in widespread use in wireless networks, since in a general multi-hop network, MAC-layer and network-layer issues will take on an increasingly important role, particularly with regard to the management of complexity when there are many simultaneous flows in the network [Huo16].
One of the key issues in PNC is how to deal with the asynchronies between the signals transmitted simultaneously by the two end nodes [Lu12]. Symbols transmitted by the two end nodes could potentially arrive at the receiver with symbol misalignment as well as relative carrier-phase offset. This could result in significant penalties to performance. Reliability of transmission is also one of the challenges that face PNC. Channel coding is typically used to solve this issue, and its application to PNC is the subject of research today.
With this in mind, PNC is the future of NC in wireless networks and thus it is important we understand it. Having given this overview, we shall now look at some of the applications that have been realised using NC in wireless networks in the next section
It is unlikely that incorporating network coding at the physical layer will be practical in the near future, for a variety of reasons detailed in [Huo16]. It is however quite feasible to build network coding into overlay networks [Magli13]. In overlay networks, nodes are applications running in computers and edges are the transport-level connections between computers. Overlay networks can be infrastructure-based, as shown by content distribution networks like Akamai. They can also be ad-hoc or peer-to-peer (P2P) networks of end hosts temporarily linked together to perform a particular communication task, for example file download, live broadcast, media on demand, instant messaging, conferencing, or gaming [Vukobratovic14]. In this section, we take a quick review of such applications of network coding, as well as applications to wireless and sensor networks.
Downloading files from a server to a client computer is one of the most common tasks that occurs in network communication. While the downloaded file is traditionally unicast from the server to the client, if we ignore delay, this can also be viewed as a multicast of the file from the server to a large group of clients using a proportionally large amount of buffering [Feng11]. Using this simplification, we can see that utilizing network coding could potentially increase the throughput and hence reduce the average download time. Consider, for example, downloading a file over a P2P network comprising all the nodes that are currently downloading the file. In this model, newly arriving nodes join the network by connecting to a subset of the existing nodes. According to [Feng11] the difficulty of P2P content distribution is finding an optimal block scheduling algorithm, which should minimize the file downloading time in a distributed manner. A real life example is BitTorrent, the original, and still the most popular protocol for P2P file downloading. In BitTorrent, the file is evenly divided into h pieces. Each node negotiates to obtain pieces of the file from its neighbors, until the node obtains all h pieces and can leave the network. After a node obtains a new piece, it announces this acquisition to its neighbors, so that every node knows which pieces every neighbor has. Nodes typically request a local rarest block, that is, a block that is least common among all of the node’s neighbors. Without network coding, each node would have to decide which blocks to download based solely on the information it could glean from its neighbour nodes. This could lead to it inefficiently downloading blocks, since blocks that are rare in its immediate neighbouring nodes are not necessarily rare blocks when considering the entire network. With network coding, however, since coded blocks are aggregates, all coded blocks are almost equally useful to any node and as such there is no need to locate and request global rarest blocks in the network. This prevents an information bottleneck and this decreases the file downloading time [Feng11].
Video on demand can be considered as a specialized form of file download where the pieces of the downloaded file have to arrive in order and must be decoded in near real time, taking into account some small delay. Network coding can be applied in this case by breaking the file into chunks, which can be downloaded sequentially [Montpetit10]. A similar technique can be used with live media broadcast. Earliest decoding can be used to further reduce delay. Instant messaging is also similar to live broadcast, but with a lower bit rate, since only text is usually being sent. Text messages are also more often sent in clumps or bursts, and have a less strict delay constraint. However, IM now frequently includes larger messages such as images and audio clips. Flooding, which is usually used for IM in P2P networks, is inefficient when used on larger files. Network coding can be applied in all of these cases to improve efficiency in overlay networks.
Apart from an application-level overlay network, another convenient place where network coding can be applied is a link-layer network such as a wireless mesh network. Mesh networks consist of mesh routers, which provide access to an existing infrastructure, and mesh clients, which both provide multi-hop connectivity to the mesh routers and utilize the connectivity provided by other mesh clients [Hundeboll11].We have already seen how the number of transmissions required for two wireless nodes to exchange packets through an intermediate node can be reduced from four to three using network coding [Sagduyu13]. This can be further extended to multiple hops. If a wireless node a sends a packet stream to a wireless node b over a long series of hops, then b can send an equal-rate stream of packets in the reverse direction to a for free. This means that additional transmissions on the intermediate hops would not be necessary. This could lead to significant savings in the total amount of data that needs to be transmitted [Hundeboll11].
For the final application of network coding we examine in this paper, let us consider wireless sensor networks, in which very small sensors can be spread onto surfaces, and can harvest energy from the environment, to form sensing surfaces over a built-in communication network [Rout13]. Sensor nodes are generally equipped with a radio transceiver, a microcontroller, a memory unit, and a set of transducers with which they can acquire and process data. To reduce each node’s size and energy requirements, the transceiver’s oscillator is replaced by an on-chip resonant circuit. However, the center frequency of the resonant circuit is random, which means that each node picks a random channel on which to transmit, and another random channel on which to receive. The nodes can self organize themselves to form a multi-hop network and transmit the data to a sink node [Rout13]. The throughput between any two nodes is constant if only routing is used, but grows linearly in the number of channels if network coding is used, and the radio ranges are chosen optimally. The reason network coding helps greatly here is that the randomly mixed packets can then find their way towards the destination without the need for explicitly informing nodes where their destinations are. This is especially useful since explicitly identifying routes is difficult when the graph connectivity is unknown.
In this section we have examined some of the areas where network coding can be applied in wireless networks and can broadly classify its benefits as resulting in improvement in a network's throughput, efficiency and scalability [Rout13]. Further benefits, which are beyond the scope of this paper to discuss, include improving resilience to attacks and eavesdropping as a side effect of the encoding schemes used.
From this paper we have gained a decent understanding of Network Coding and what it entails, having looked at the origins of this field through to its various applications in wireless networks. We have looked at both theoretical and practical aspects of this field and been exposed to a superficial analysis of the theory behind its numerous sub-categories. Network coding schemes such as RLNC, TNC and ONC have been thoroughly dissected and linked to their applications in improving throughput, reliability and energy efficiency in various related fields. We also took a look at research being done to apply NC at the physical level using natural properties of wireless systems. While NC has had tangible results in being applied to link and application layers, there is still some time before we may see significant use of NC schemes at the physical layer due to such issues as synchronicity. If and when that does happen however, there will surely be a significant increase in the benefits NC can provide to wireless networks. For the moment, however, NC is limited to packet-based systems, and within the field of wireless networking, to wireless mesh and sensor networks in particular.
| [Magli13] | Magli, Enrico, et al. "Network coding meets multimedia: A review." Multimedia, IEEE Transactions on 15.5 (2013): 1195-1212, URL: http://arxiv.org/pdf/1211.4206.pdf |
| [Shen12] | Shen, Hang, et al. "An adaptive opportunistic network coding mechanism in wireless multimedia sensor networks." International Journal of Distributed Sensor Networks 2012 (2012), URL: http://www.hindawi.com/journals/ijdsn/2012/565604/abs/ |
| [Liew13] | Liew, Soung Chang, Shengli Zhang, L. Lu, "Physical-layer network coding: Tutorial, survey, and beyond." Physical Communication 6 (2013): 4-42, URL: http://arxiv.org/pdf/1105.4261.pdf |
| [Rout13] | Rout, Rashmi Ranjan, Soumya K. Ghosh. "Enhancement of lifetime using duty cycle and network coding in wireless sensor networks." Wireless Communications, IEEE Transactions on 12.2 (2013): 656-667, URL: http://www.cs.bgu.ac.il/~segal/PAPERS/06399490.pdf |
| [Feng11] | Feng, Chen, and Baochun Li. "1 Network Coding for Content Distribution and Multimedia Streaming in Peer-to-Peer Networks." Network Coding: Fundamentals and Applications (2011): 61.., URL: https://www.researchgate.net/profile/Chen_Feng9/publication/267839813_Network_Coding_for_Content_Distribution_and_Multimedia_Streaming_in_Peer-to-Peer_Networks/links/54a163080cf256bf8baf6bb9.pdf |
| [Vukobratovic14] | Vukobratovic, Dejan, et al. "Random network coding for multimedia delivery services in LTE/LTE-Advanced." Multimedia, IEEE Transactions on 16.1 (2014): 277-282, URL: http://strathprints.strath.ac.uk/47699/5/Vukobratovic_etal_TM2014_random_network_coding_for_multimedia_delivery.pdf |
| [Ostovari16] | Ostovari, Pouya, Jie Wu. "Robust wireless transmission of scalable coded videos using two-dimensional network coding." Computer Networks 95 (2016): 115-126, URL: http://astro.temple.edu/~tuc71330/publications_files/Robust%20Wireless%20Transmission%20of%20Scalable%20Coded%20Videos%20using%20Inter-layer%20Network%20Coding.pdf |
| [Huo16] | Huo, Qiang, et al. "Source and Physical-Layer Network Coding for Correlated Two-Way Relaying." IET Communications (2016) 160-182, URL: http://arxiv.org/pdf/1602.00132.pdf |
| [Qureshi12] | Qureshi, Jalaluddin, Chuan Heng Foh, and Jianfei Cai. "Optimal solution for the index coding problem using network coding over GF (2)." Sensor, Mesh and Ad Hoc Communications and Networks (SECON), 2012 9th Annual IEEE Communications Society Conference on. IEEE, 2012, URL: http://arxiv.org/pdf/1209.6539v1.pdf |
| [Lu12] | Lu, Lu, Soung Chang Liew. "Asynchronous physical-layer network coding." Wireless Communications, IEEE Transactions on 11.2 (2012): 819-831, URL: http://arxiv.org/pdf/1105.3144.pdf |
| [Bassoli13] | Bassoli, Riccardo, et al. "Network coding theory: A survey." Communications Surveys & Tutorials, IEEE 15.4 (2013): 1950-1978, URL: http://romisatriawahono.net/lecture/rm/survey/network%20security/Bassoli%20-%20Network%20Coding%20Theory%20-213.pdf |
| [Sagduyu13] | Sagduyu, Yalin E., Randall A. Berry, Dongning Guo. "Throughput and stability for relay-assisted wireless broadcast with network coding." Selected Areas in Communications, IEEE Journal on 31.8 (2013): 1506-1516, URL: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.418.4879&rep=rep1&type=pdf |
| [Ahlswede00] | Ahlswede, Rudolf, et al. "Network information flow." Information Theory, IEEE Transactions on 46.4 (2000): 1204-1216, URL: http://www.cs.cornell.edu/courses/cs783/2007fa/papers/acly.pdf |
| [Wiki1] | “Linear Network Coding”, Wikipedia: The Free Encyclopedia. Wikimedia Foundation, URL: https://en.wikipedia.org/wiki/Linear_network_coding |
| [Hundeboll11] | Hundebøll, Martin, and Jeppe Ledet-Pedersen. "Inter-Flow Network Coding." (2011), URL: https://downloads.open-mesh.org/batman/papers/batman-adv_network_coding.pdf |
| [Montpetit10] | Montpetit, Marie-José, and Muriel Médard. "Video-centric network coding strategies for 4G wireless networks: an overview." Consumer Communications and Networking Conference (CCNC), 2010 7th IEEE. IEEE, 2010, URL: https://www.researchgate.net/profile/Muriel_Medard/publication/224119209_Video-Centric_Network_Coding_Strategies_for_4G_Wireless_Networks_An_Overview/links/0c96052ef0f063dc16000000.pdf |