 |
Chunlei Liu, Raj Jain
Department of Computer and Information Science
The Ohio State University, Columbus, OH 43210-1277, USA
email: {cliu, jain}@cse.wustl.edu
Computer networks use congestion feedback from the routers and destinations to control the transmission load. Delivering timely congestion feedback is essential to the performance of networks. Reaction to the congestion can be more effective if faster feedback is provided. Current TCP/IP networks use timeout, duplicate ACKs and explicit congestion notification (ECN) to deliver the congestion feedback, each provides a faster feedback than the previous method. In this paper, we propose a mark-front strategy that delivers an even faster congestion feedback. With analytical and simulation results, we show that mark-front strategy reduces buffer size requirement, improves link efficiency and provides better fairness among users.
Keywords:Explicit Congestion Notification, mark-front, congestion control, buffer size requirement, fairness.
Computer networks use congestion feedback from the routers and destinations to control the transmission load. When the feedback is ``not congested'', the source slowly increases the transmission window. When the feedback is ``congested'', the source reduces its window to alleviate the congestion [ 1]. Delivering timely congestion feedback is essential to the performance of networks. The faster the feedback is, the more effective the reaction to congestion can be.
TCP/IP networks uses three methods -- timeout, duplicate ACKs and ECN -- to deliver congestion feedback.
In 1984, Jain [ 2] proposed to use timeout as an indicator of congestion. When a packet is sent, the source starts a retransmission timer. If the acknowledgment is not received within a certain period of time, the source assumes congestion has happened and the packet has been lost because of the congestion. The lost packet is retransmitted and the source's congestion window is reduced. Since it has to wait for the timer to expire, timeout turns out to be the slowest feedback.
With duplicate ACKs, the receiver sends an acknowledgment after the reception of a packet. If a packet is not received but its subsequent packet arrives, the ACK for the subsequent packet is a duplicate ACK. TCP source interprets the reception of three duplicate ACKs as an indication of packet loss. Duplicate ACKs avoid the long wait for the retransmission timer to expire, and therefore, delivers a faster feedback than timeout.
Both timeout and duplicate ACKs methods send congestion feedback at the cost of packet losses, which not only increase the traffic in the network, but also add large transfer delay. Studies [ 3, 4, 5, 6, 7] show that the throughput of the TCP connection is limited by packet loss probability.
The congestion feedbacks from timeout and duplicate ACKs are implicit because they are inferred by the networks. In timeout method, incorrect timeout value may cause erroneous inference at the source. In duplicate ACKs method, all layers must send the packets in order. If some links have selective local link-layer retransmission, like those used in wireless links to combat transmission errors, the packets are not delivered in order. The inference of congestion from duplicate ACKs us no longer valid.
Ramakrishnan and Jain's work in [ 8], which has been popularly called the DECbit scheme, uses a single bit in the network layer header to signal the congestion. The Explicit Congestion Notification (ECN) [ 9, 10], motivated by the DECbit scheme, provides a mechanism for intermediate routers to send early congestion feedback to the source before actual packet losses happen. The routers monitor their queue length. If the queue length exceeds a threshold, the router marks the Congestion Experiencedbit in the IP header. Upon the reception of a marked packet, the receiver marks the ECN-Echobit in the TCP header of the acknowledgment to send the congestion feedback back to the source. In this way, ECN delivers an even faster congestion feedback explicitly set by the routers.
In most ECN implementations, when congestion happens, the congested router marks the incoming packet. When the buffer is full or when a packet needs to be dropped as in Random Early Detection (RED), some implementations have the ``drop from front'' option to drop packets from the front of the queue, as suggested in Yin [ 12] and Lakshman [ 13]. However, none of these implementations mark the packet from the front of the queue.
In this paper, we propose the ``mark-front'' strategy. When a packet is sent from a router, the router checks whether its queue length is greater than the pre-determined threshold. If yes, the packet is marked and sent to the next router. The mark-front strategy differs from the current ``mark-tail'' policy in two ways. First, the router marks the packet in the front of the queue and not the incoming packet, so the congestion signal does not undergo the queueing delay as the data packets. Second, the router marks the packet at the time when it is sent, and not at the time when the packet is received. In this way, a more up-to-date congestion feedback is given to the source.
The mark-front strategy also differs from the ``drop from front'' option, because when packets are dropped, only implicit congestion feedback can be inferred from timeout or duplicate ACKs. When packets are marked, explicit and faster congestion feedback is sent to the source.
Our study finds that, by providing faster congestion feedback, mark-front strategy reduces the buffer size requirement at the routers; it avoids packet losses and thus improves the link efficiency when the buffer size in routers is limited. Our simulations also show that mark-front strategy improves the fairness among old and new users, and alleviates TCP's discrimination against connections with large round trip times.
This paper is organized as follows. In section 2 we describe the assumptions for our analysis. Dynamics of queue growth with TCP window control is studied in section 3. In section 4, we compare the buffer size requirement of mark-front and mark-tail strategies. In section 5, we explain why mark-front is fairer than mark-tail. In section 6, the simulation results that verify our conclusions are presented.
In [ 9], ECN is proposed to be used with average queue length and RED. The purpose of average queue length is to avoid sending congestion signals caused by bursty traffic, and the purpose of RED is to desynchronize sender windows [ 14, 15] so that the router can have a smaller queue. Because average queue length and RED are difficult to analyzed mathematically, in this paper we assume a simplified congestion detection criterion: when the actual queue lengthis smaller than the threshold, the incoming packet will not be marked; when the actual queue lengthexceeds the threshold, the incoming packet will be marked.
We also make the following assumptions. (1) Receiver windows are large enough so the bottleneck is in the network. (2) Senders always have data to send. (3) There is only one bottleneck link that causes queue buildup. (4) Receivers acknowledge every packet received and there are no delayed acknowledgments. (5) The queue length is measured in packets and all packets have the same size.
In this section, we study the relationship between the window size at the source and the queue size at the congested router. The analysis is made on one connection, simulation results of multiple connections will be presented in section 6.
Under the assumption of one bottleneck, when congestion happens, packets pile up only at the bottleneck router. The following lemma is obvious.
Denote the source window size at time tas w(t), then we have
| Q(t)=w(t-t p )-rd. | (1) |
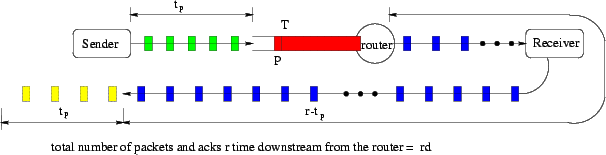
ProofConsider the packet that arrives at the congested router at time t. It was sent by the source at time t-t p . At that time, the number of packets on the forward path and outstanding ACKs on the reverse path was w(t-t p ). By time t, t p dACKs are received by the source. All packets between the source and the router have entered the congested router or have been sent downstream. As shown in Figure 1, the pipe length from the congested router to the receiver, and back to the source is r-t p . The number of downstream packets and outstanding ACKs are (r-t p )d. The rest of the w(t-t p ) unacknowledged packets are still in the congested router. So the queue length is
| Q(t)=w(t-t p )-t p d- (r-t p )d= w(t-t p )-rd. | (2) |
This finishes the proof.
Notice that in this theorem, we did not use the number of packets between the source and the congested router to estimate the queue length, because the packets downstream from the congested router and the ACKs on the reverse path are equally spaced, but the packets between the source and the congested router may not be.
ECN feedback can be used to achieve zero-loss congestion control. If routers have enough buffer space and the threshold value is properly set, the source can control the queue length by adjusting its window size based on the ECN feedback. The buffer size requirement will be the maximum queue size that can be reached before the window reduction takes effect. In this section, we use Theorem 1 to study the buffer size requirement of mark-tail and mark-front strategies.
Suppose Pis the packet that increased the queue length over the threshold T, and it was sent from the source at time s 0 and arrived at the congested router at time t 0 . Its acknowledgment, which was an ECN-echo, arrived at the source at time s 1 and the window was reduced at the same time. We also assume that the last packet before the window reduction was sent at time s 1 - and arrived at the congested router at time t 1 - .
If Tis reasonably large (about rd) such that the buildup of a queue of size Tneeds rtime, the assumption in Theorem 1 is satisfied, we have
| T=Q(t 0 )=w(t 0 -t p )-rd= w(s 0 )-rd. | (3) |
|
|
(4) |
Since the time elapse between s
0
and s
1
is one RTT, if packet Pwere not marked, the congestion window would increase to 2w(s
0
). Because Pwas marked, when the ECN-Echo is received, the congestion window was
|
|
(5) |
Upon the receipt of ECN-Echo, the congestion window was halved. The source can not send any more packets before half of the packets are acknowledged. So 2T+rd-1 is the maximum queue length.
When Tis large, the bound 2T+rd-1 is tight. Since the queue length in congestion avoidance phase is smaller, this bound is actually the buffer size requirement.
Suppose Pis the packet that increased the queue length over the threshold T, and it was sent from the source at time s 0 and arrived at the congested router at time t 0 . The router marked the packet P' that stood in the front of the queue. The acknowledgment of P', which was an ECN-echo, arrived at the source at time s 1 and the window was reduced at the same time. We also suppose the last packet before the window reduction was sent at time s 1 - and arrived at the congested router at time t 1 - .
If Tis reasonably large (about rd) such that the buildup of a queue of size Tneeds rtime, the assumption in Theorem 1 is satisfied. We have
| T=Q(t 0 )=w(t 0 -t p )-rd= w(s 0 )-rd, | (7) |
|
|
(8) |
In slow start phase, the source increases the congestion window by one for every acknowledgment it receives. If there were no congestion, upon the reception of the acknowledgment of P, the congestion window would be doubled to 2w(s
0
). However, when the acknowledgment of P' arrived, T-1 acknowledgments corresponding to packets prior to Pwere still on the way. So the window size at time s
1
-
was
|
|
(9) |
Upon the receipt of ECN-Echo, congestion window is halved. The source can not send any more packets before half of the packets are acknowledged. So T+rdis the maximum queue length.
When Tis large, the bound T+rdis tight. Since the queue length in congestion avoidance phase is smaller, this bound is actually the buffer size requirement.
Theorem 2 and 3 estimate the buffer size requirement for zero-loss ECN congestion control. They show that the mark-front strategy reduces the buffer size requirement by rd, a bandwidth round trip time product.
Contrary to the mark-tail policy, the mark-front strategy marks packets already in the buffer. Flows with large buffer occupancy have higher probability to be marked. Flows with smaller buffer occupancy will less likely to be marked. Therefore, old flows will back off to give part of their buffer room to the new flow. This helps to prevent the lock-out phenomenon. Therefore, mark-front strategy is fairer than mark-tail strategy.
TCP's discrimination against connections with large RTTs is also well known. The cause of this discrimination is similar to the discrimination against new connections. Connections with small RTTs receives their acknowledgment faster and therefore grow faster. Starting at the same time as connections with large RTTs, connections with small RTTs will take larger room in the buffer. With mark-tail policy, packets already in the queue will not be marked but only newly arrived packets will be marked. Therefore, connections with small RTTs will grow even larger, but connections with large RTTs have to back off. Mark-front alleviates this discrimination by treating all packets in the buffer equally. Packets already in the buffer may also be marked. Therefore, connections with large RTTs can have larger bandwidth.
In order to compare the mark-front and mark-tail strategies, we performed a set of simulations with the nssimulator [ 11].
Our simulations are based on the basic simulation model shown in Figure
2. A number of sources
![]() are connected to the router r
1
by 10 Mbps links. Router r
1
is connected to r
2
by a 1.5 Mbps link. Destinations
are connected to the router r
1
by 10 Mbps links. Router r
1
is connected to r
2
by a 1.5 Mbps link. Destinations
![]() are connected to r
2
by 10 Mbps links. The link speeds are chosen so that congestion will only happen at the router r
1
, where mark-tail and mark-front strategies are tested.
are connected to r
2
by 10 Mbps links. The link speeds are chosen so that congestion will only happen at the router r
1
, where mark-tail and mark-front strategies are tested.
With the basic configuration, the fixed round trip time, including the propagation time and the processing time at the routers, is 59 ms. Changing the propagation delay between router r 1 and r 2 from 20 ms to 40 ms gives an RTT of 99 ms. Changing the propagation delays between the sources and router r 1 gives us configurations of different RTTs. An FTP application runs on each source. The data packet size is 1000 bytes and the acknowledgment packet size is 40 bytes. TCP Reno and ECN are used for congestion control.
The following simulation scenarios are designed on the basic simulation model. In each of the scenarios, if not otherwise specified, all connections have an RTT of 59 ms, start at 0 second and stop at the 10th second.
Scenarios 1, 4, 6 and 7 are mainly designed for testing the buffer size requirement. Scenarios 1, 3, 4, 6, 7, 8 are for link efficiency, and scenarios 2, 3, 4, 5, 6, 7 are for fairness among users.
We use three metrics to compare the the results. The first metric is the buffer size requirementfor zero loss congestion control, which is the maximum queue size that can be built up at the router in the slow start phase before the congestion feedback takes effect. If the buffer size is greater or equal to this value, the network will not suffer packet losses. The analytical results for one connection are given in Theorem 2 and 3. Simulations will be used in multiple-connection and different RTT cases.
The second metric, link efficiency, is calculated from the number of acknowledged packets and the possible number of packets that can be transmitted during the simulation time. There are two reasons that cause the link efficiency to be lower than full utilization. The first reason is the slow start process. In the slow start phase, the congestion window grows from one and remains smaller than the network capacity until the last round. So the link is not fully used in slow start phase. The second reason is low threshold. If the congestion detection threshold Tis too small, ECN feedback can cause unnecessary window reductions. Small congestion window leads to link under-utilization. Our experiments are long enough so that the effect of the slow start phase can be minimized.
The third metric, fairnessindex, is calculated according to the method described in [
17]. If mconnections share the bandwidth and x
i
is the throughput of connection i, the fairnessindex is calculated as:
|
|
(11) |
When all connections have the same throughput, the fairness index is 1. The farther the throughput distribution is away from the equal distribution, the smaller the fairness value is. Since the fairness index in our results is often close to 1, in our graphs, we draw the
unfairnessindex:
| unfairness= 1- fairness, | (12) |
The operations of ECN depend on the threshold value T. In our results, all three metrics are drawn for different values of threshold.
 |
 |
 |
One single connection |
Two connections with different RTTs |
Five connections with different RTTs |
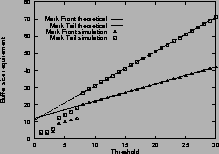
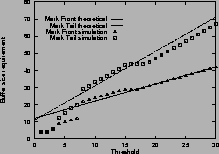
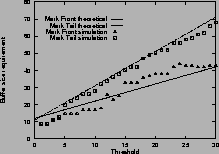
Figure
3shows the buffer size requirement for mark-tail and mark-front strategies. The measured maximum queue lengths are shown with ``
![]() '' and ``
'' and ``
![]() ''. The corresponding analytical estimates from Theorem 2 and 3 are shown with dashed and solid lines. Figure
3 (a) shows the buffer size requirement for one single connection with an RTT of 59 ms. Figure
3 (b) shows the requirement for two connections with different RTTs. Figure
3 (c) shows the requirement for five connections with different RTTs. When the connections have different RTTs, the analytical estimate is calculated from the smallest RTT.
''. The corresponding analytical estimates from Theorem 2 and 3 are shown with dashed and solid lines. Figure
3 (a) shows the buffer size requirement for one single connection with an RTT of 59 ms. Figure
3 (b) shows the requirement for two connections with different RTTs. Figure
3 (c) shows the requirement for five connections with different RTTs. When the connections have different RTTs, the analytical estimate is calculated from the smallest RTT.
From these results, we find that for connections with equal RTTs, the analytical estimate of buffer size requirement is accurate. When threshold Tis small, the buffer size requirement is an upper bound, when
![]() , the upper bound is tight. For connections with different RTTs, the estimate given by the largest RTT is an upper bound, but is usually an overestimate. The estimate given by the smallest RTT is a closer approximation.
, the upper bound is tight. For connections with different RTTs, the estimate given by the largest RTT is an upper bound, but is usually an overestimate. The estimate given by the smallest RTT is a closer approximation.
 |
 |
 |
One single connection |
Two overlapping connections |
Two same connections, limited buffer |
 |
 |
 |
Five connections with same RTT |
Five connections with different RTTs |
Five same connections, limited buffer |
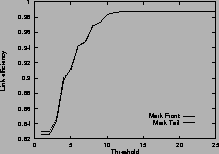
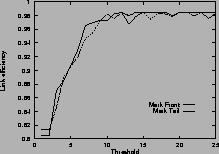
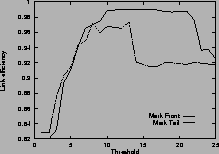
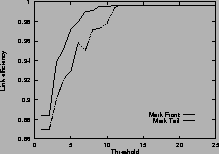
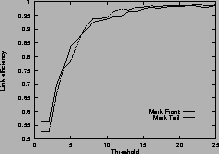
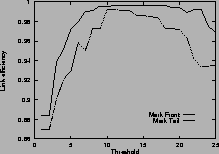
Figure 4shows the link efficiency. Results for mark-front strategy are drawn with solid line, and results for mark-tail strategy are drawn with dashed line. In most cases, when the router buffer size is large enough, mark-front and mark-tail have comparable link efficiency, but when the threshold is small, mark-front have slightly lower efficiency because congestion feedback is sent to the source faster. For the same value of threshold, faster feedback translates to more window reductions and longer link idling.
When the router buffer size is small, as in Figure 4 (c) and Figure 4 (f), mark-front has better link efficiency. This is because mark-front sends congestion feedback to source faster, so the source can reduce its window size sooner to avoid packet losses. Without spending time on the retransmissions, mark-front strategy can improve the link efficiency.
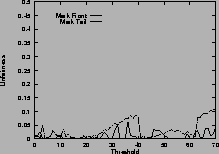
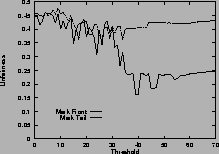
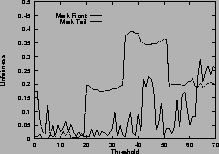
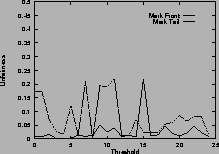
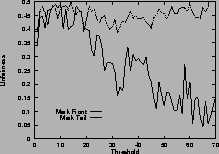
Figure 5shows the unfairness. Again, results for mark-front strategy are drawn with solid line, and results for mark-tail strategy are drawn with dashed line. In Figure 5 (a), the two connections have the same configuration. Which connection receives more packets than the other is not deterministic, so the unfairness index seems random. However, in general, mark-front is fairer than mark-tail.
 |
 |
 |
Two same connections |
Two overlapping connections |
Two connections with different RTTs |
 |
 |
 |
Five same connections |
Five same connections, limited buffer |
Five connections with different RTTs |
In Figure 5 (b), the two connections are different: the first connection starts first, occupies the buffer room and locks out the second connection. Although they have the same time span, the second connection receives fewer packets than the first. Mark-front avoids this lock-out phenomenon and improves the fairness. In addition, as the threshold increases, the unfairness index of mark-tail increases, but the mark-front remains roughly the same, regardless of the threshold. Results for five same connections are shown in Figure 5 (d).
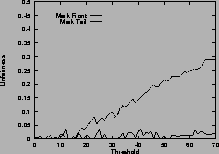
Figure 5 (c) shows the difference on connections with different RTTs. With mark-tail strategy, the connections with small RTTs grow faster and therefore locked out the connections with large RTTs. Mark-front strategy avoids the lock-out problem and alleviate the discrimination against connections with large RTT. The difference of the two strategies is obvious when the threshold is large. Results for five connections with different RTTs are shown in Figure 5 (f).
Figure 5 (e) shows the unfairness when the router buffer size is limited. In this scenario, the mark-tail strategy marks the incoming packet when the queue length exceeds the threshold, and drops the incoming packet when the buffer is full. The mark-front strategy, on the other hand, marks and drops the packets from the front of the queue when necessary. The results show mark-front strategy is fairer than mark-tail.
In this paper we study the mark-front strategy used in ECN. Instead of marking the packet from the tail of the queue, this strategy marks the packet in the front of the queue and thus delivers faster congestion feedback to the source. Our study reveals mark-front's three advantages over mark-tail policy. First, it reduces the buffer size requirement at the routers. Second, when the buffer size is limited, it reduces packet losses and improves the link efficiency. Third, it improves the fairness among old and new users, and helps to alleviate TCP's discrimination against connections with large round trip times.
With a simplified model, we analyze the buffer size requirement for both mark-front and mark-tail strategies. Link efficiency, fairness and more complicated scenarios are tested with simulations. The results show that mark-front strategy has better performance than the current mark-tail policy.
All our papers and ATM Forum contributions are available through http://www.cse.wustl.edu/~jain/index.html