Bobby Vandalore, Raj Jain, Rohit Goyal, Sonia Fahmy
The Ohio State University
Department of Computer and Information Science
Columbus, OH 43210-1277
E-mail: {vandalor, jain, goyal, fahmy}@cse.wustl.edu
ABR rate allocation schemes can achieve high link utilizations by maintaining non-zero (small) queues in the steady state, and draining queues when the sources do not have data to send. The queue length (and queuing delays) can be controlled if part of the available bandwidth is used for draining queues in the event of queue build up. A simple threshold function can allocate such bandwidth to drain queues. Better control of the queues, and hence delay, can be achieved using more sophisticated queue control functions. We study the design and analysis of several such queue control functions: the step, linear, hyperbolic and inverse hyperbolic functions. Analytical explanation and simulation results consistent with analysis are presented. From the study, we conclude that the inverse hyperbolic is the best queue control function. To reduce complexity, the linear function can be used since it performs satisfactorily in most cases. 1
The goals of rate allocation schemes include maintaining high link utilizations, small queuing delays, low cell loss, and fairness among competing sources. In order to support (low quality) video sources over the ABR service, it is also desirable that, in the steady state, the rates and queuing delays not be highly variable. One way to achieve high utilization and low queuing delay is to vary the target ABR rate as a function of the queue lengths.
In this paper, we study several queue control functions which satisfy the above requirements. We present an analytical explanation for the performance of these functions, and give simulation results consistent with the analysis. The convergence time and behavior of the queues in the steady state are used as metrics to evaluate the queue control functions.
In this section, the relationship between the queue length and queue control function is derived. This section also discusses the design considerations of queue control functions. The following terms are used in the discussion:
X(t) denotes that X is a function of time. We assume that the
explicit rate switch scheme operates at the output port and gives
feedback to source i according to the following equation: Target
rate
![]() ,
where HPR is the
total rate of high priority traffic such as VBR and CBR. For
simplicity, we ignore higher priority traffic such as CBR and VBR, and
assume that Rl is same as the link rate Rlink. The function
f(Q) is the queue control function. The queue length increases if
f(Q) > 1; remains constant if f(Q) = 1; and decreases if f(Q) <
1. Hence, by using an appropriate function f(Q), the queue length
can be controlled.
,
where HPR is the
total rate of high priority traffic such as VBR and CBR. For
simplicity, we ignore higher priority traffic such as CBR and VBR, and
assume that Rl is same as the link rate Rlink. The function
f(Q) is the queue control function. The queue length increases if
f(Q) > 1; remains constant if f(Q) = 1; and decreases if f(Q) <
1. Hence, by using an appropriate function f(Q), the queue length
can be controlled.
![]()
The switch scheme tries to adjust the input rate R(t) to match the
output rate depending on the current queue size, i.e.,
![]() .
We assume no higher priority
traffic, so
.
We assume no higher priority
traffic, so
![]() .
.
The sources adjust their rates ri(t) based on the explicit rate feedback from the switch. The feedback reaches the switch after time tp. Hence, ri(t) (source rate) can be expressed using the following equation:
![]() .
.
Since
tf = 2 tp, we get:
![]() .
.
For the ERICA+ scheme, the above function is as follows:
![]() .
.
For other schemes, the following modification can be done to
incorporate queue control. Let erA(t) be the explicit rate
calculated by an algorithm A. Then queue control can be incorporated
by adding the following as last step in the algorithm A:
![]() ,
where PCR is the peak
cell rate. It can be shown that if the algorithm A converges to
max-min rates, then the modified algorithm also converges to the
max-min rate.
,
where PCR is the peak
cell rate. It can be shown that if the algorithm A converges to
max-min rates, then the modified algorithm also converges to the
max-min rate.
1. If the queue length is very small, it should be increased, so that the scheme can maintain small queues which can drained when the link is under utilized. This implies that f(Q) should be greater than one for small queue lengths.
2. In the steady state, we want the queue length to be almost constant, and the computed rate to be the max-min fair rate. The function Q(t) satisfies the goal of constant queue length if f(Q) = 1 in the steady state. If the switch scheme is fair, the steady state rates will be max-min fair.
3. If the queue is large, then part of the link capacity must be used to drain the queues. Hence f(Q) should be less than one. It is desirable not to use all the capacity to drain the queue. Therefore, there is a minimum threshold, queue drain limit factor (QDLF), for f(Q).
4. The f(Q) function has to be continuous. Discontinuities imply sudden changes which give rise to oscillations of rates and queues.
The queue control function with above properties will be of the form
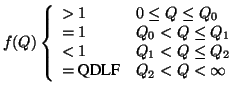
The curve used in the control function in the underload region is
called the ``a-curve'' and the one used in the overload region is called
the ``b-curve''. The parameters used in the a-curve
![]() are called a-parameters;
are called a-parameters;
![]() are called the b-parameters. Since all the
functions are continuous, at Q2 we have the equation
f(Q2) =
QDLF. So, Q2 can be expressed in terms of QDLF and
a-parameters for linear, hyperbolic and inverse hyperbolic functions.
are called the b-parameters. Since all the
functions are continuous, at Q2 we have the equation
f(Q2) =
QDLF. So, Q2 can be expressed in terms of QDLF and
a-parameters for linear, hyperbolic and inverse hyperbolic functions.
The change in queue length in an averaging interval ts is given by:
Initial behavior: In the beginning, the queue lengths grow depending on the initial cell rate (ICR) value. So the maximum queue depends on the ICR and round trip time and is independent of the queue control function used. The feedback information reaches the sources and the sources adjust their rates accordingly.
Under-utilization: The switch scheme initially estimates that the link is under utilized. The queue control function evaluates to f(Q) > 1, during under utilization (Q < Q0). Thus the switch gives feedback to the sources to increase their rates, which increases queue length at the switch. The rate of increase of the queue length is dictated by the b-curve of the queue control function.
Overload: Either due to the increase in the source
rates or the high ICRs, an overload condition occurs and queues at the
switch grow. Initially, the feedback information is not accurate; hence,
the queue might grow beyond the Q2 threshold. In such a heavy overload
condition, the queues are quickly drained by using the (1-QDLF) fraction of
link capacity. In the meantime, the feedback control loop is
established, and the switch gives reliable feedback to the
sources. For the mild overload region, i.e., queue length in range of
![]() ,
the a-curve is the queue control function. The
value of f(Q) is less than one in this region, which effectively
decreases the queue length.
,
the a-curve is the queue control function. The
value of f(Q) is less than one in this region, which effectively
decreases the queue length.
Steady state: The feedback tries to match the input rate to the output rate. As the input rate approaches the output rate, the oscillations die down and the network reaches the steady state. In the steady state, the rates and the queue lengths remain constant since f(Q) = 1.
For all four queue control functions, f(Q) > 1 in the range
![]() ,
and f(Q) < 1 in the range
,
and f(Q) < 1 in the range
![]() .
The change in
queue length depends on the value of f(Q) - 1. Hence, the change in
the queue length is an additive increase for the underutilized region
[
4
]. The queue length converges to a value in between Q0and Q1. An interesting point to note is that the amount of increase
and the amount of decrease itself is dictated by the current queue
length and the difference between the current queue length and the
steady state queue length.
.
The change in
queue length depends on the value of f(Q) - 1. Hence, the change in
the queue length is an additive increase for the underutilized region
[
4
]. The queue length converges to a value in between Q0and Q1. An interesting point to note is that the amount of increase
and the amount of decrease itself is dictated by the current queue
length and the difference between the current queue length and the
steady state queue length.
If the condition Q0 < Q(t) < Q1 is satisfied and the input rate matches the output rate, then the steady state is achieved, and the queue remains at this constant length.
If Q1 < Q(t) < Q2, then Q(t) starts decreasing with slope -(1-sa). This decrease also takes place for tf time, if the queue length is between Q0 and Q1, and if the input rate is close to the output rate then again the steady state is achieved.
Therefore, for the system to achieve the steady state, the value of
the queue length after one feedback interval should be within the
range Q0 and Q1. This requirement is satisfied if the condition
![]() holds. Since the step
function has discontinuities, it is very sensitive to the queue length
value near the thresholds and the steady state might not be reached if
the parameters are not set properly. In such a case, the queue grows
from a value below Q0 for duration tf seconds, crosses Q1 and
decreases for tf seconds to a value less than Q0. This pattern
repeats giving rise to periodic oscillations.
holds. Since the step
function has discontinuities, it is very sensitive to the queue length
value near the thresholds and the steady state might not be reached if
the parameters are not set properly. In such a case, the queue grows
from a value below Q0 for duration tf seconds, crosses Q1 and
decreases for tf seconds to a value less than Q0. This pattern
repeats giving rise to periodic oscillations.
| Queue | a | b | Q1 | Q2 | Conv | Avg |
| Control | val | val | (secs) | QLen | ||
| Simple | 0.75 | 1.01 | 4 | 26 | - | 252.93 |
| 0.90 | 1.01 | 4 | 26 | - | 98.04 | |
| 0.90 | 1.05 | 4 | 26 | - | 663.63 | |
| 0.95 | 1.01 | 4 | 26 | - | 251.51 | |
| 0.95 | 1.05 | 4 | 26 | - | 124.11 | |
| 0.95 | 1.01 | 2 | 26 | - | 896.90 | |
| 0.95 | 1.01 | 8 | 26 | - | 483.20 | |
| Linear | 1/16 | 1/16 | 2 | 26 | 0.20 | 311.85 |
| 1/16 | 1/16 | 4 | 26 | 0.32 | 403.52 | |
| 1/16 | 1/16 | 8 | 26 | 0.61 | 402.85 | |
| Hyper- | 1.15 | 1.05 | 2 | 26 | - | 509.94 |
| bolic | 1.15 | 1.05 | 4 | 26 | 0.32 | 214.19 |
| 1.15 | 1.05 | 8 | 26 | 0.82 | 220.96 | |
| Inv. | 36 | 1.05 | 2 | 26 | 0.22 | 313.17 |
| Hyper- | 16.5 | 1.05 | 4 | 26 | 0.25 | 209.50 |
| bolic | 6.75 | 1.05 | 8 | 26 | 1.12 | 202.27 |
The mean and standard deviation of the rates and the queue lengths are calculated for every 100 milliseconds. In steady state, the oscillations are small, so the standard deviation is small compared to mean. The quantity (mean + standard deviation) has a value close to the mean in the steady state. The convergence time was calculated based on the (mean + standard deviation) graphs (given in [ 9 ]).
For the step function, there is oscillation in both rates and queue length. For linear and hyperbolic functions, the oscillations die down and the system reaches steady state. In steady state, the rate and queue length are constant and utilization is 100%. Hence, the linear, hyperbolic and inverse hyperbolic queue control functions fulfill the desired goal. This is consistent with the analytical explanation given in the previous section. In all the cases when the queue length and the rates converge, the queue length is non-zero and hence the utilization at steady state is 100%.
The following parameters were used in the simulations for this
configuration. The thresholds used were Q0 = 176,
![]() ,
,
![]() ,
QDLF = 0.5. The values of a-param and
b-param were, for the step function,
sa = 0.95,
sb = 1.01; for
the linear function
ma = 1/16,
mb = 1/16; for the hyperbolic
function
ha = 1.15,
mb = 1.05; and for the inverse hyperbolic
function
,
QDLF = 0.5. The values of a-param and
b-param were, for the step function,
sa = 0.95,
sb = 1.01; for
the linear function
ma = 1/16,
mb = 1/16; for the hyperbolic
function
ha = 1.15,
mb = 1.05; and for the inverse hyperbolic
function
![]() ,
,
![]() .
.
Table 3 shows the performance for the four queue control functions. The table shows the H(1) VC's mean rate, switch queue length for SW5 and its convergence time, and standard deviation before one second and after one second. The queue length variation is present in all the three cases. The rate variation is much less in linear and hyperbolic and inverse hyperbolic functions compared to step function.
| Queue | Quantity | Convg. | Mean |
| Control | time(secs) | ||
| Step | |||
| H(1) ACR | - | 72.81 | |
| SW5 Queue | - | 284.28 | |
| Linear | H(1) ACR | 1.25 | 52.46 |
| SW5 Queue | 1.3 | 455.46 | |
| Hyper | H(1) ACR | 1.45 | 52.77 |
| SW5 Queue | 1.3 | 361.32 | |
| Inv.Hyper | H(1) ACR | 1.51 | 52.38 |
| SW5 Queue | 2.0 | 1443.72 |
Figures 4 and 5 were obtained by simulating the GFC-2 configuration using the step, linear and hyperbolic and inverse hyperbolic queue control functions. Graphs 4 (a), 4 (c), 5 (a) and 5 (c) show the ACR rate for one VC of each of A through H type VCs versus time when different queue control functions are used. From these graphs, it can be seen that the expected rates are obtained when linear, hyperbolic and inverse hyperbolic functions are used for queue control. The (b) and (d) graphs have the queue length for all the switches. The maximum queue is due to the initial overload,
|
|
|
|
before the first round trip time. Once the feedback control loop is established, the f(Q) value is QDLF and queues are drained quickly.
When the step function (figure 4 (a)) is used, the oscillations are more compared to the oscillations when other functions are used. Some of the VCs do not get their max-min fair share rates and the VCs near the fair share have considerable oscillations. The step function is very sensitive to queue length variation near the thresholds. Since the configuration is complex with large number of VCs passing through each of the switches, the queue length and hence the rates vary. For the graphs 4 (c), 5 (a) and 5 (c) the oscillations are only present before steady state. The oscillations die down and the rates become steady since the function f(Q) changes smoothly. The maximum queue length is same for all queue control functions since this depends only on the ICR. When the inverse hyperbolic function is used, the queues are larger since in this case the steady state queue length is near Q1.
The simulation results obtained by using different queue control functions in the simple and the GFC-2 configurations are consistent with the analytical explanation. The step function is sensitive to queue thresholds ( Q0,Q1,Q2). The other functions are not sensitive to these queue thresholds. Small steady state queuing delay can be achieved by choosing nearby values for Q0 and Q1.
In this paper, we have considered the problem of designing a simple and robust queue control function for switch schemes. A switch scheme tries to maximize utilization, minimize queuing delay and give max-min fair rates to the sources. It is also desirable to have fewer oscillations in rates and queue lengths to support (low quality) video over ABR service. We assume a switch scheme model which dynamically adjusts the rate of the sources to match the output rate and drain large queues. The design considerations were discussed with analytical explanations. Four different queue control functions were analyzed. The choice of parameters for the queue control functions was both explored analytically and by simulation. The simulations showed that even in complex configurations (like GFC-2), the system behavior was consistent with the analytical explanation. When the step function is used, the system oscillates and does not converge in most cases. Both the analytical and the simulation results show that the inverse hyperbolic is the best queue control function, followed by the hyperbolic and the linear queue control functions. For lower implementation complexity, the linear function is recommended.